Durbin Watson Table
"DW Table"
by : Danny Prasetyo Hartanto & Desi Wulandari (2024)
Durbin Watson Tabel atau DW Table (tabel Durbin Watson / Tabel DW) merupakan pembanding bagi Durbin Watson Statistic (nilai DW) pada saat pengambilan keputusan dalam pengujian autokorelasi.
Autokorelasi adalah salah satu asumsi klasik yang melekat pada analisis regresi salah satunya adalah regresi linier yang digunakan untuk menguji independensi dari series residual. atau definisi yang umum adalah menguji ada / tidaknya hubungan (korelasi) yang sangat kuat antar series residual.
Salah satu teknik pengujian autokorelasi adalah Durbin Watson (DW). Konsep Durbin Watson (DW) adalah menghitung korelasi antara series residual pada derajat pertama (ρ(et-et-1)), yaitu korelasi residual periode saat ini dengan residual satu periode sebelumnya (lag 1) dengan formula sebagai berikut :
yang mana :
et = residual / error / disturbance periode saat ini
et-1 = residual / error / disturbance satu periode sebelumnya
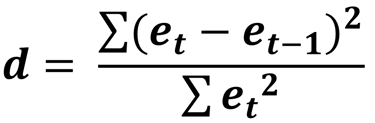
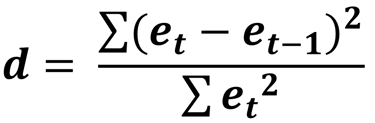
Kritera pengujian atau kriteria pengambilan keputusan yang menggunakan statistik uji Durbin Watson adalah sebagai berikut :
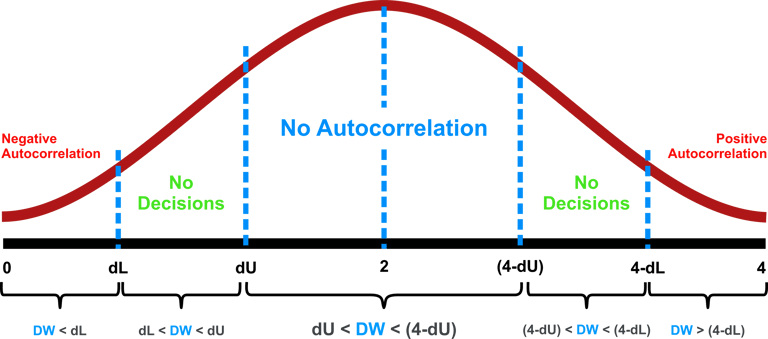
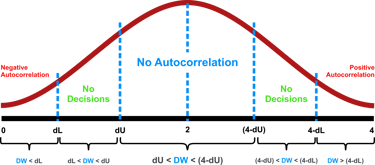
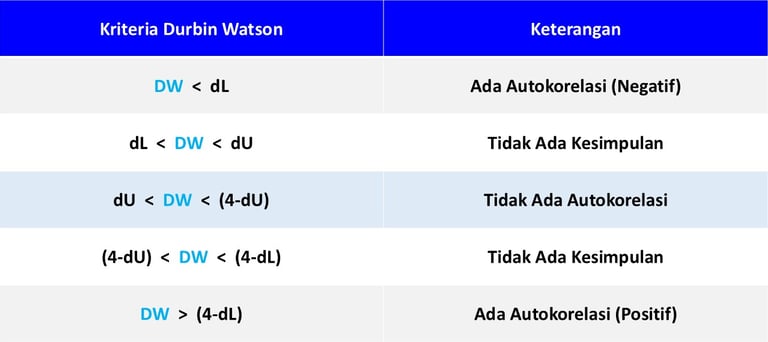
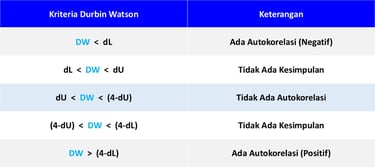
Keterangan :
DW = Durbin Watson
dL = Durbin Lower (Batas bawah nilai durbin tabel)
dU = Durbin Upper (Batas atas nilai durbin tabel)
Atau jika kriteria tersebut disajikan dalam bentuk tabel maka kriteria pengujian statistik Durbin Watson adalah sebagai berikut :
Untuk mendapatkan skor Durbin Watson (DW) tabel secara mudah dan instan, peneliti dapat mengakses
InQuest Calculator Durbin Watson (DW) tabel berikut :
Untuk mendapatkan skor Durbin Watson (DW) tabel secara mudah dan instan, peneliti dapat mengakses InQuest Calculator Durbin Watson (DW) tabel berikut :
Untuk mendapatkan nilai Durbin Watson (DW) tabel secara manual, peneliti dapat menggunakan tabel Durbin Watson (tabel DW)
Klik shortcut sesuai dengan alpha (α), sampel / observasi (n) dan banyaknya variabel independen (k) yang anda butuhkan
Untuk mendapatkan nilai Durbin Watson (DW) tabel secara manual, peneliti dapat menggunakan tabel Durbin Watson (tabel DW)
Klik shortcut sesuai dengan alpha (α), sampel / observasi (n) dan banyaknya variabel independen (k) yang anda butuhkan
Tabel DW dengan Alpha 1% ; n = 1 - 125
Tabel DW dengan Alpha 1% ; n = 250 - 2000
Tabel DW dengan Alpha 1% ; n = 126 - 245
Tabel DW dengan Alpha 5% ; n = 1 - 125
Tabel DW dengan Alpha 5% ; n = 250 - 2000
Tabel DW dengan Alpha 5% ; n = 126 - 245
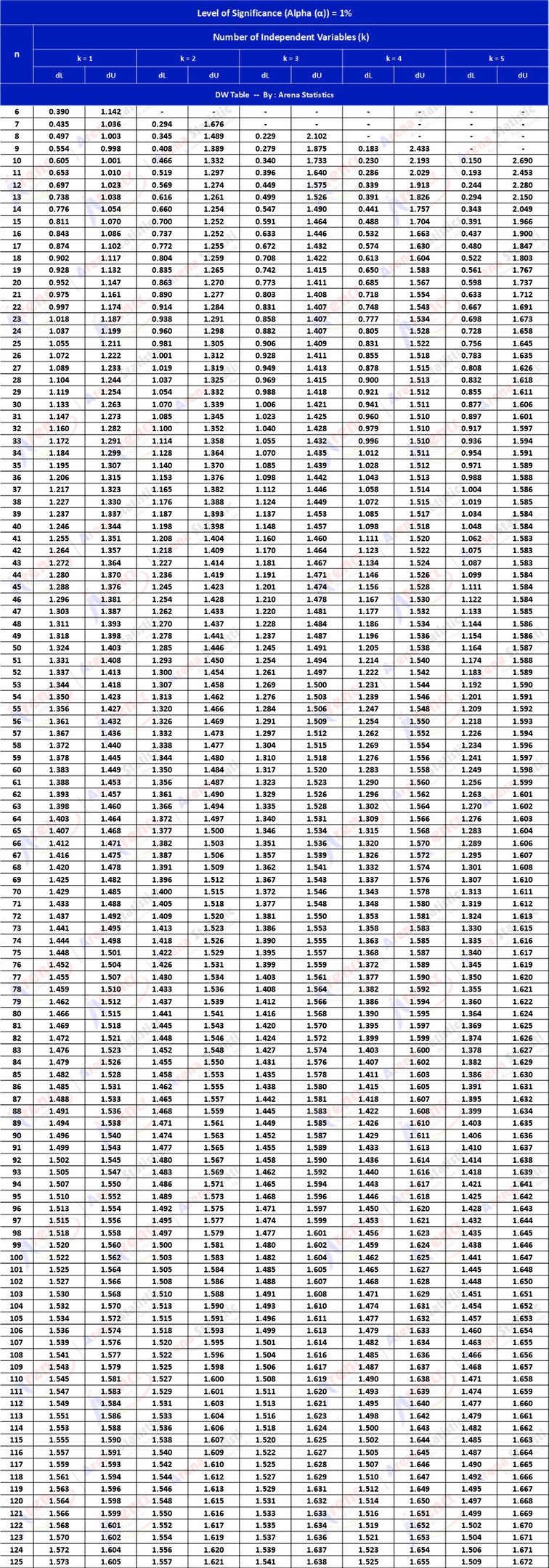
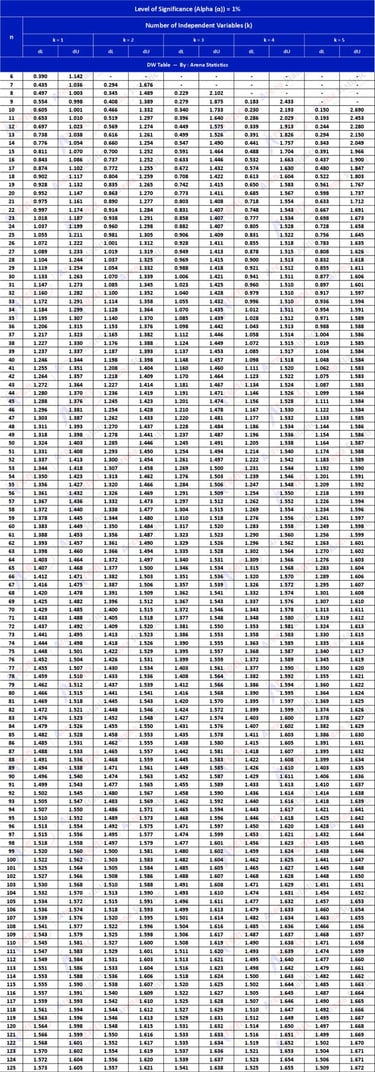
DW Tabel dengan Alpha 1% ; observasi (n) = 6 - 125 ; k = 1 - 5
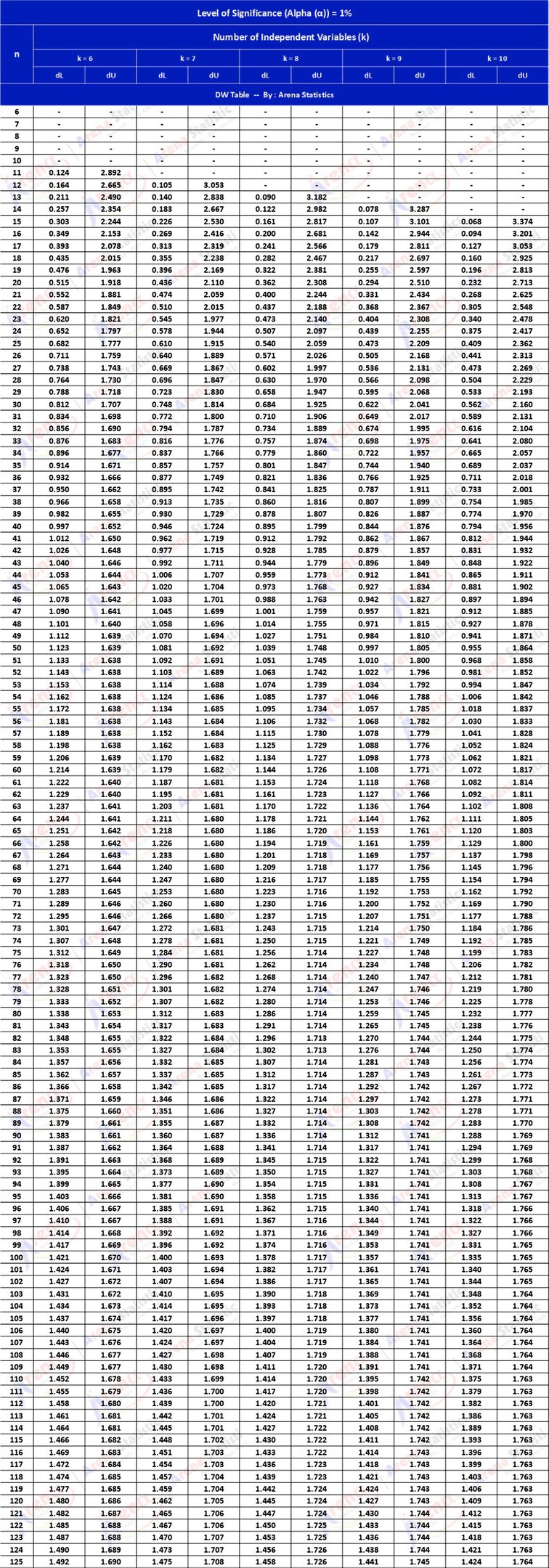
DW Tabel dengan Alpha 1% ; observasi (n) = 6 - 125 ; k = 6 - 10
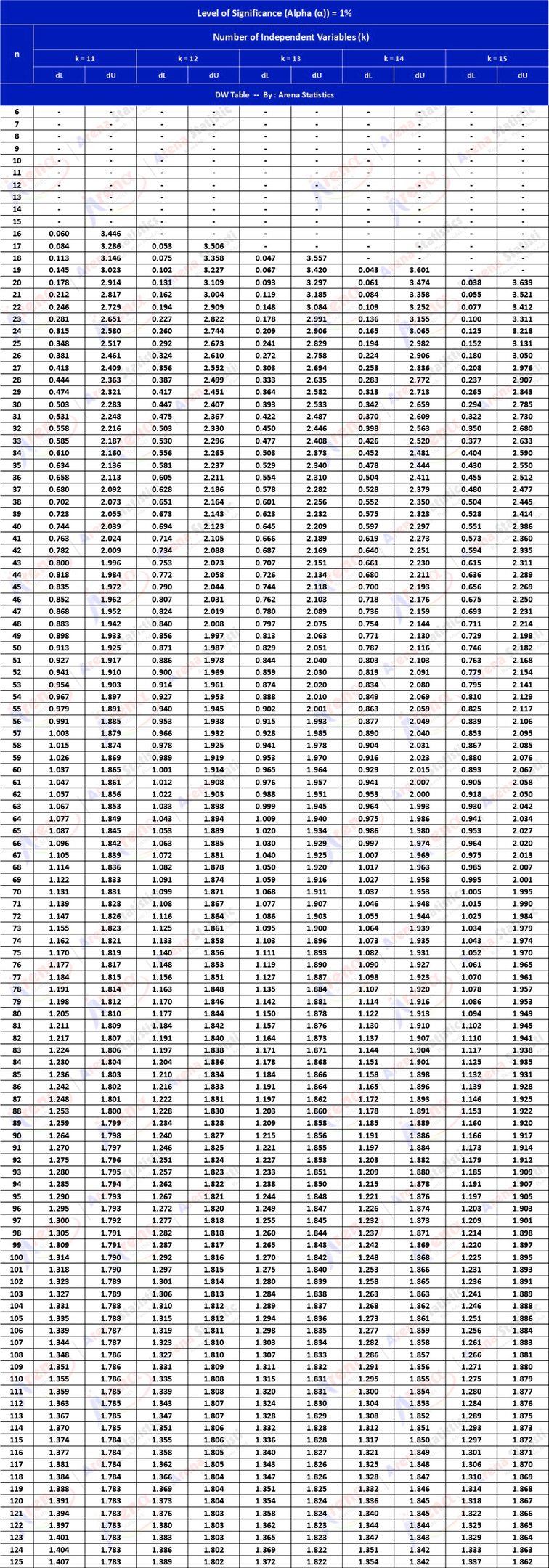
DW Tabel dengan Alpha 1% ; observasi (n) = 6 - 125 ; k = 11 - 15
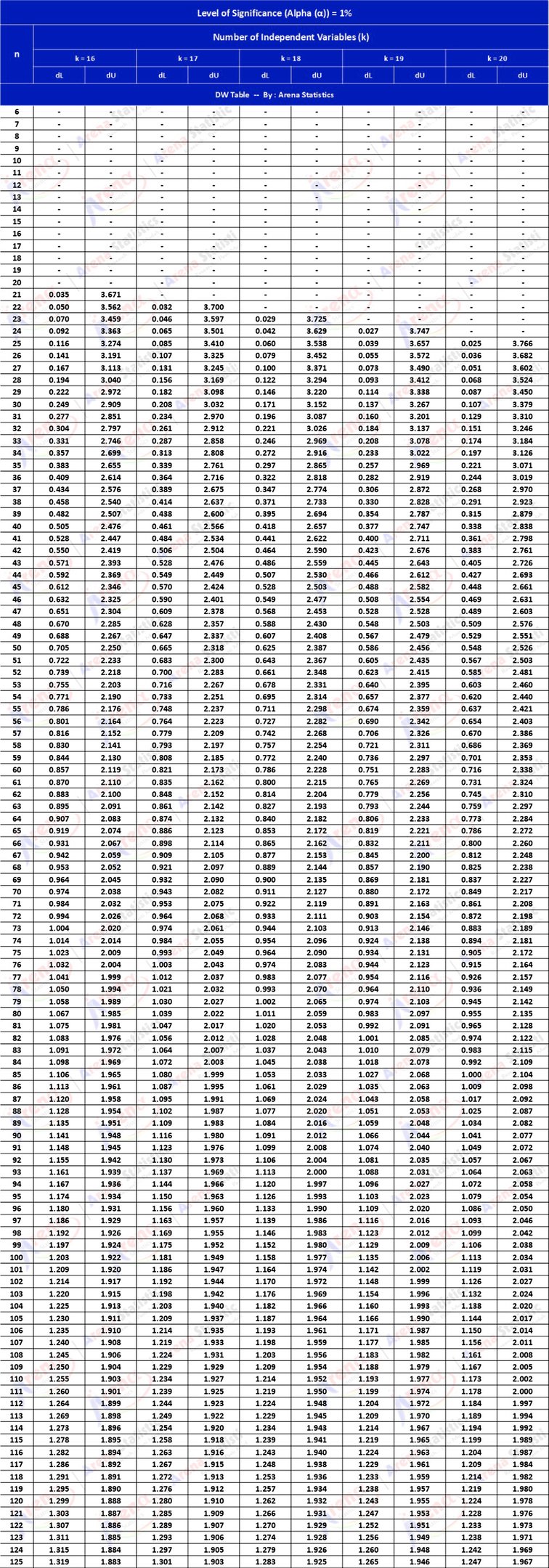
DW Tabel dengan Alpha 1% ; observasi (n) = 6 - 125 ; k = 16 - 20
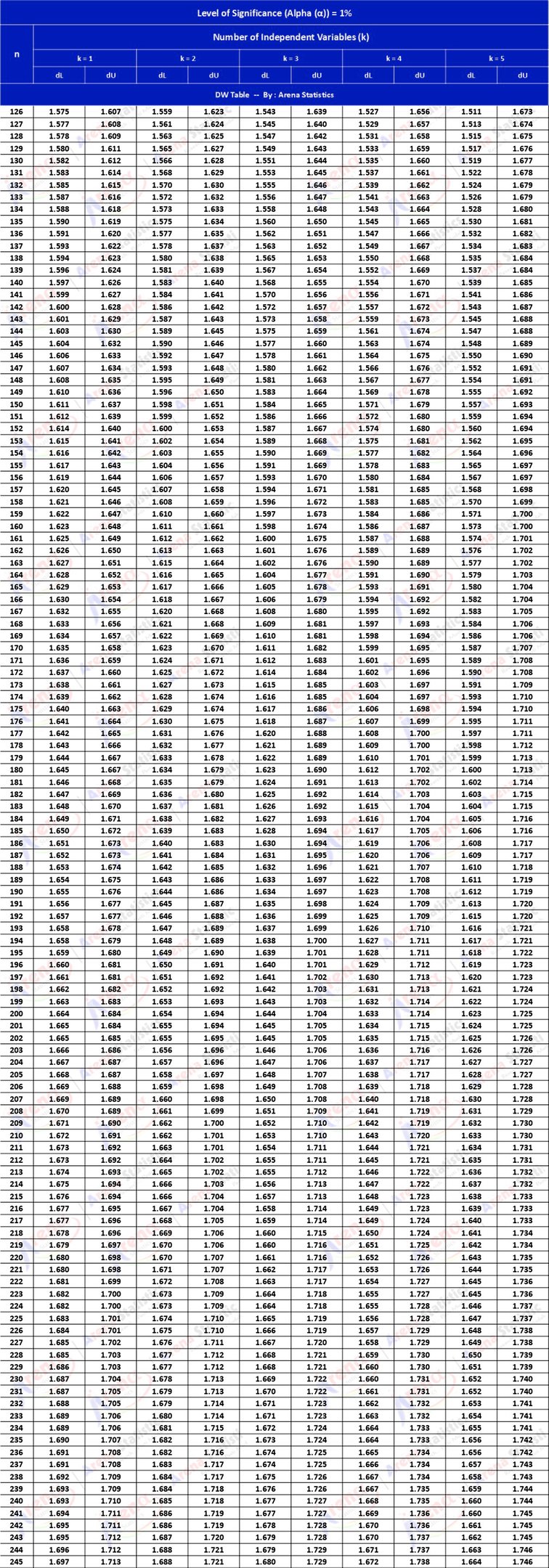
DW Tabel dengan Alpha 1% ; observasi (n) = 126 - 245 ; k = 1 - 5
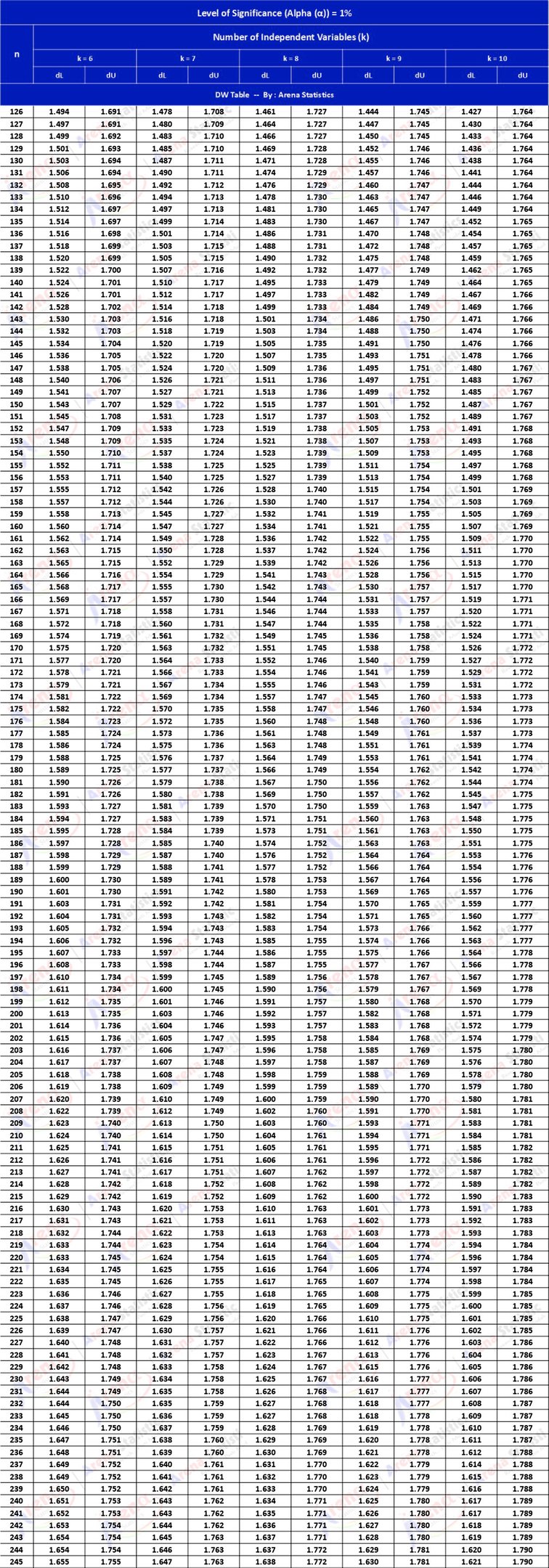
DW Tabel dengan Alpha 1% ; observasi (n) = 126 - 245 ; k = 6 - 10
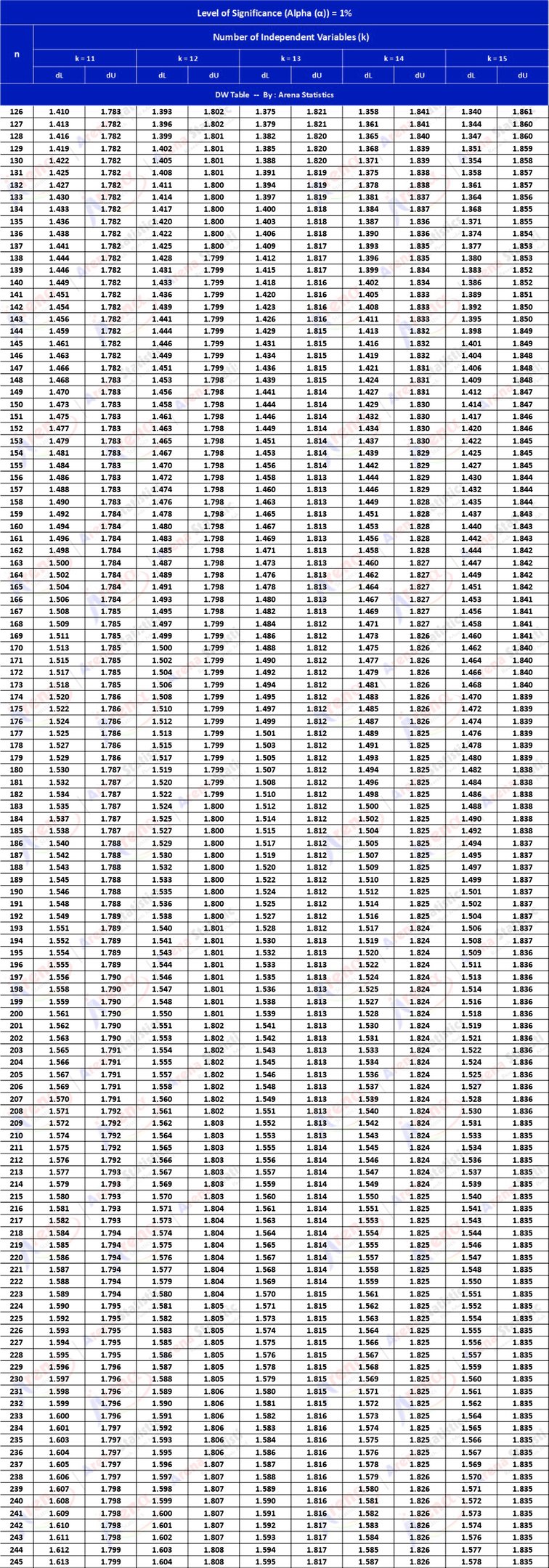
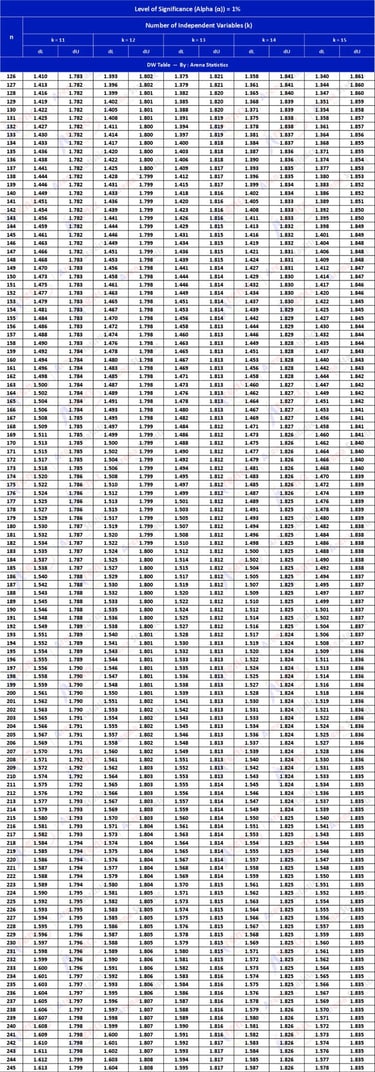
DW Tabel dengan Alpha 1% ; observasi (n) = 126 - 245 ; k = 11 - 15
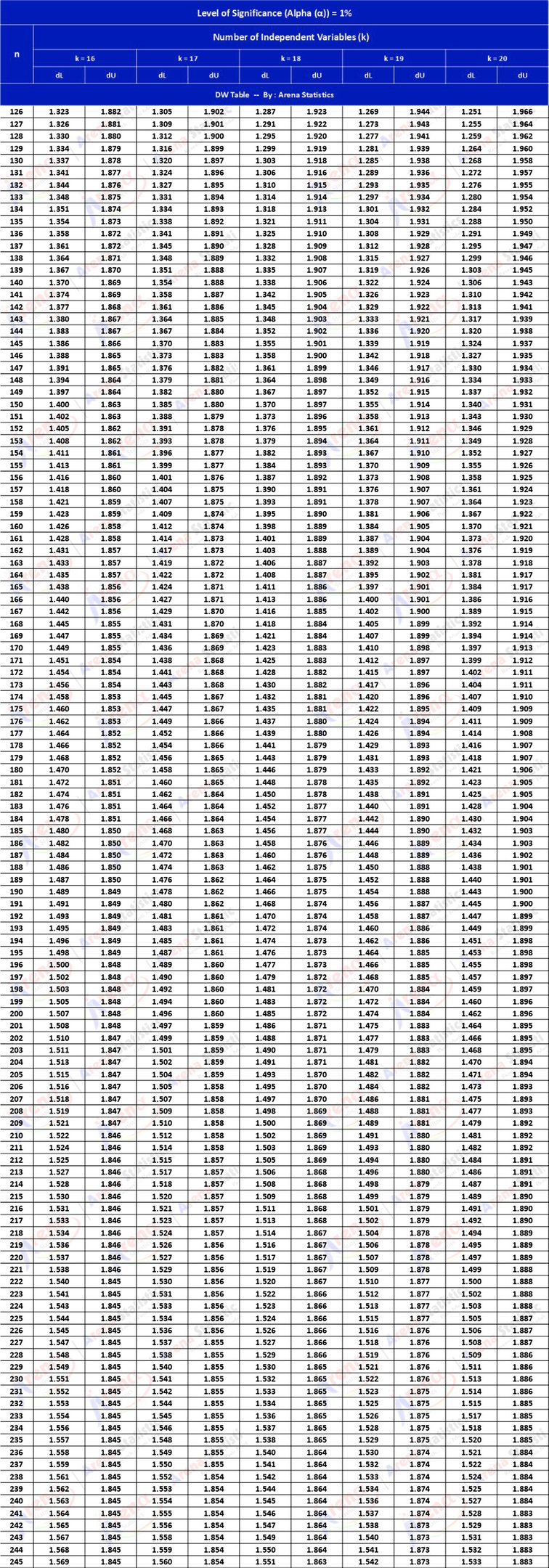
DW Tabel dengan Alpha 1% ; observasi (n) = 126 - 245 ; k = 16 - 20
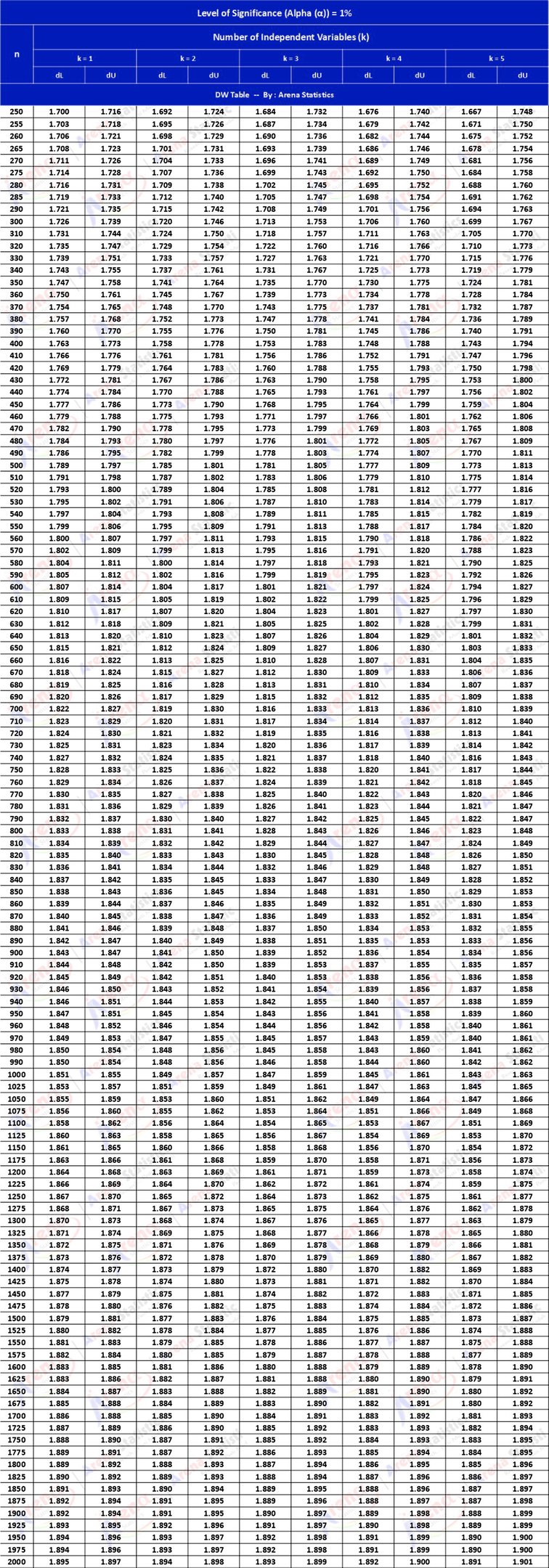
DW Tabel dengan Alpha 1% ; observasi (n) = 250 - 2000 ; k = 1 - 5
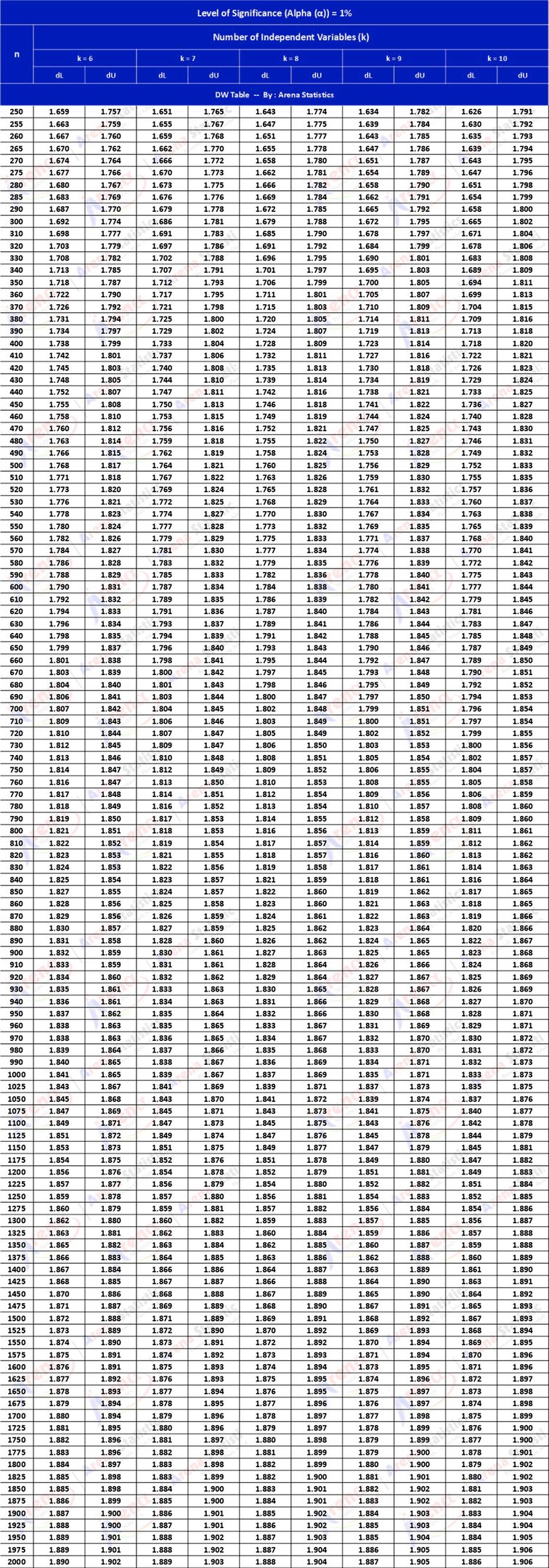
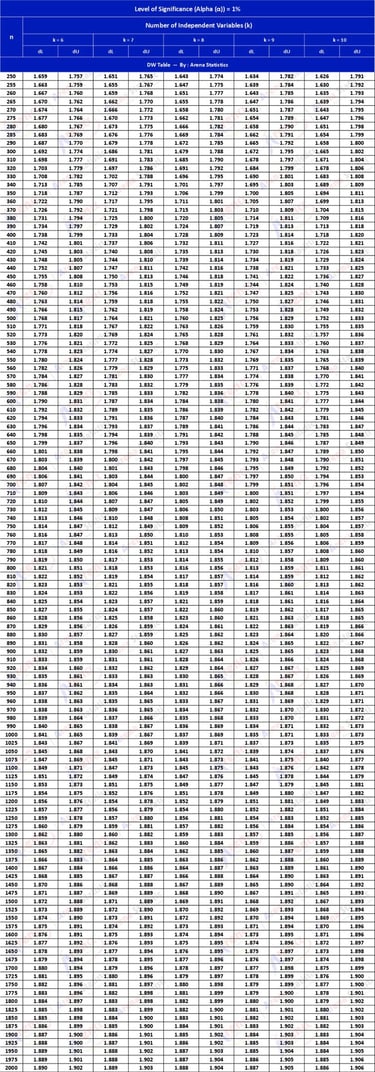
DW Tabel dengan Alpha 1% ; observasi (n) = 250 - 2000 ; k = 6 - 10
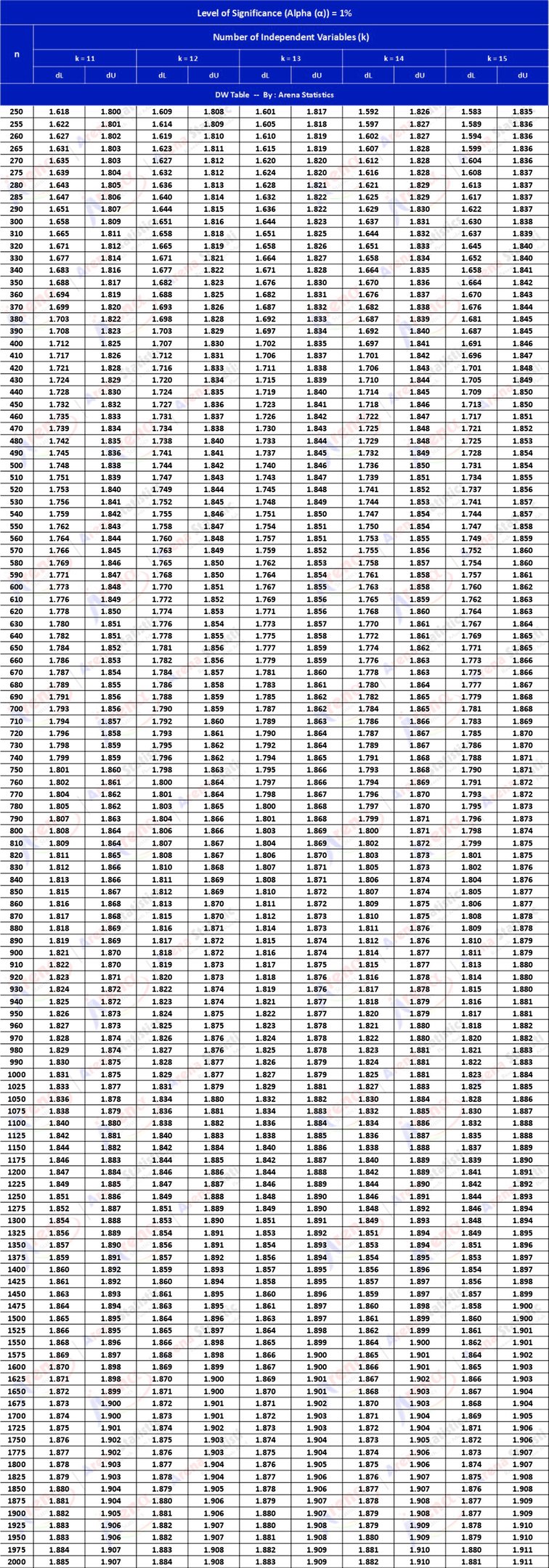
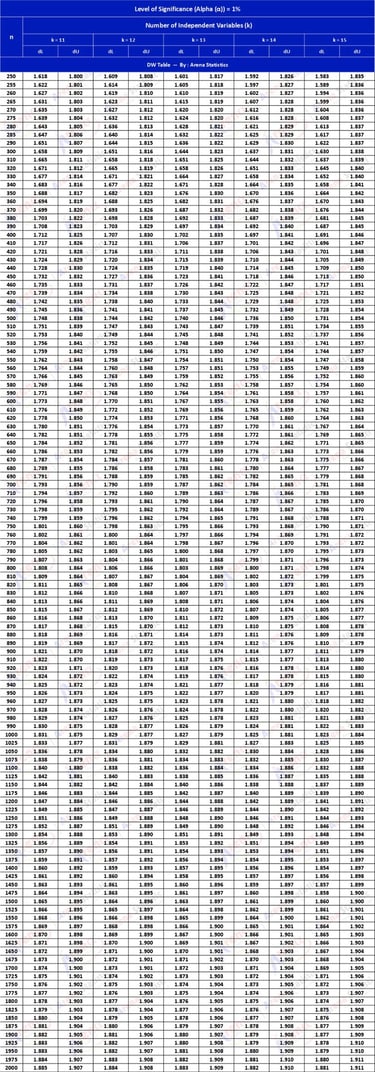
DW Tabel dengan Alpha 1% ; observasi (n) = 250 - 2000 ; k = 11 - 15
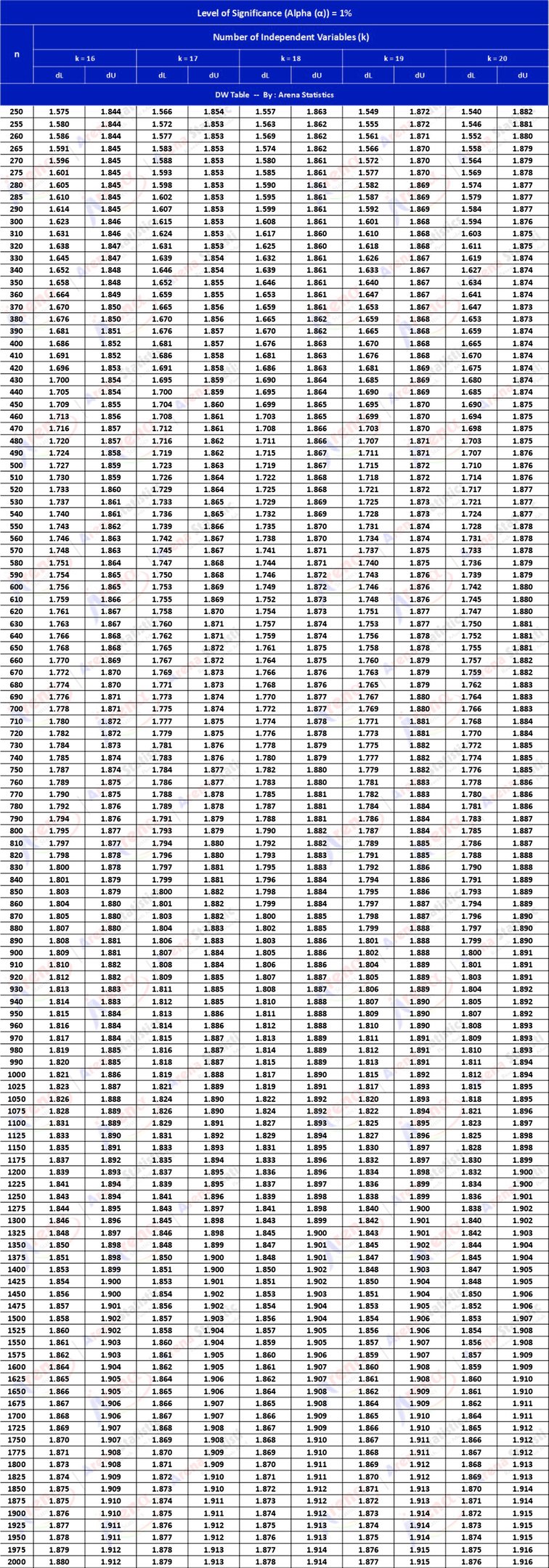
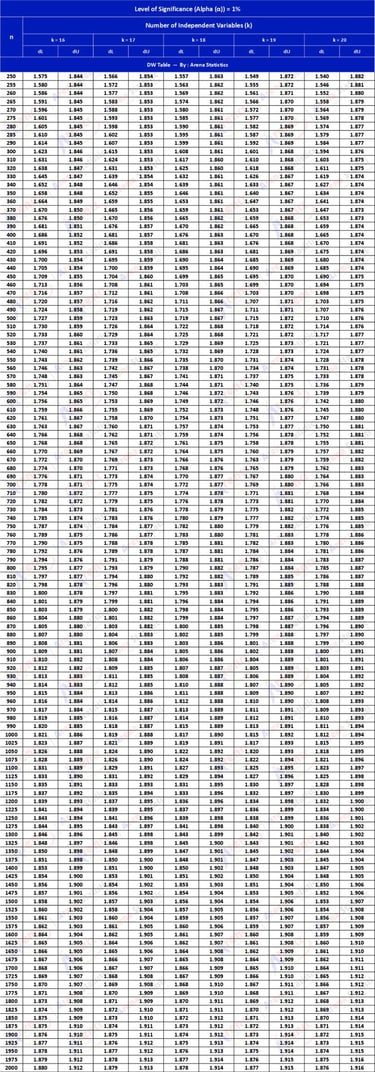
DW Tabel dengan Alpha 1% ; observasi (n) = 250 - 2000 ; k = 16 - 20
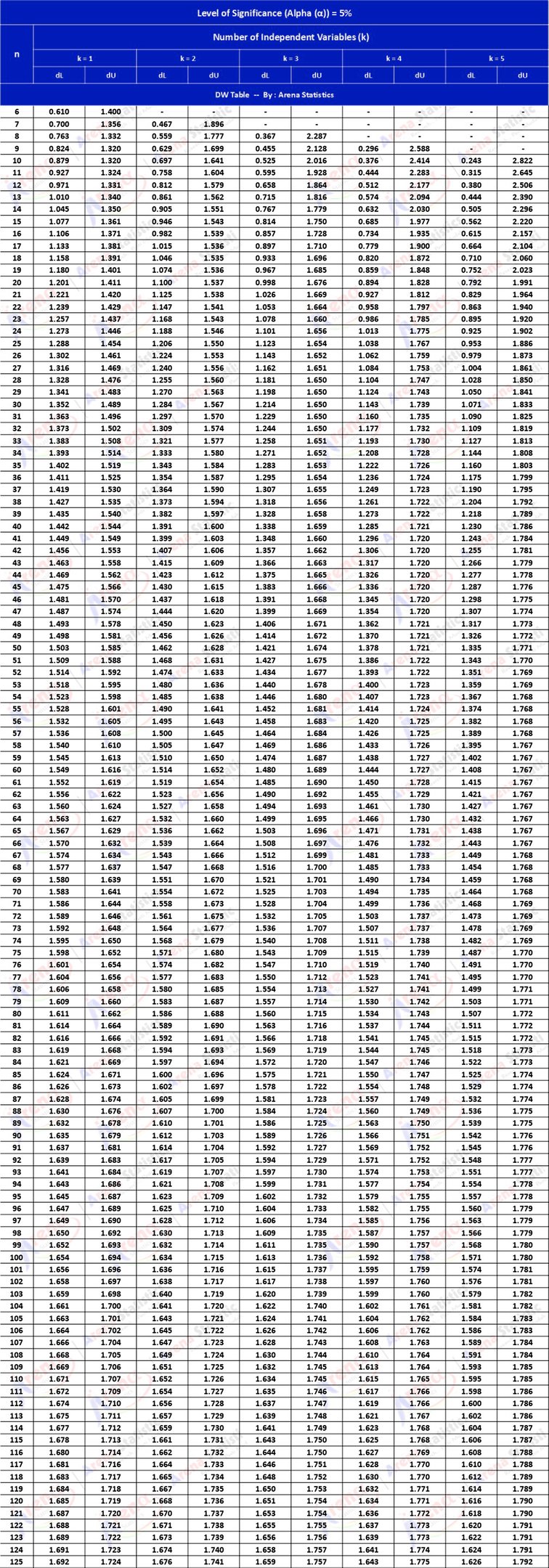
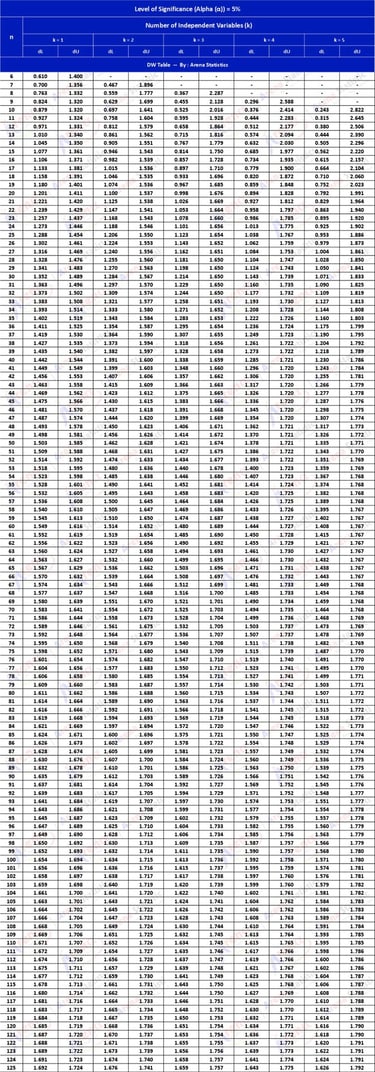
DW Tabel dengan Alpha 5% ; observasi (n) = 6 - 125 ; k = 1 - 5
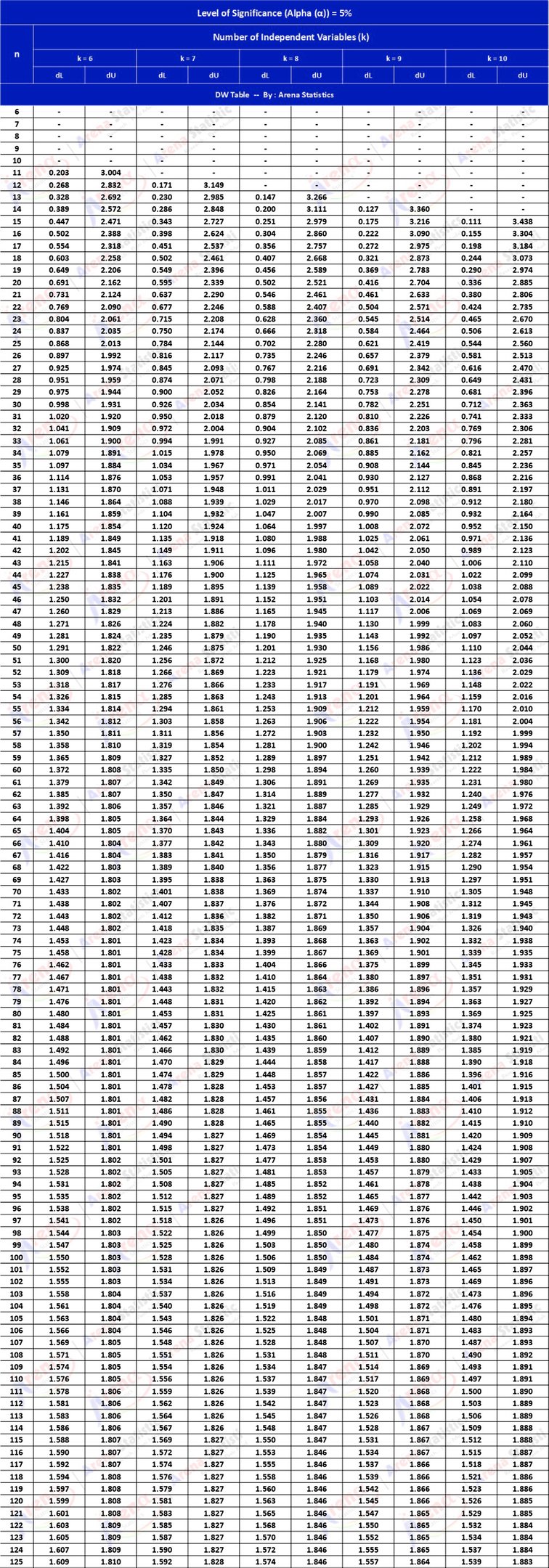
DW Tabel dengan Alpha 5% ; observasi (n) = 6 - 125 ; k = 6 - 10
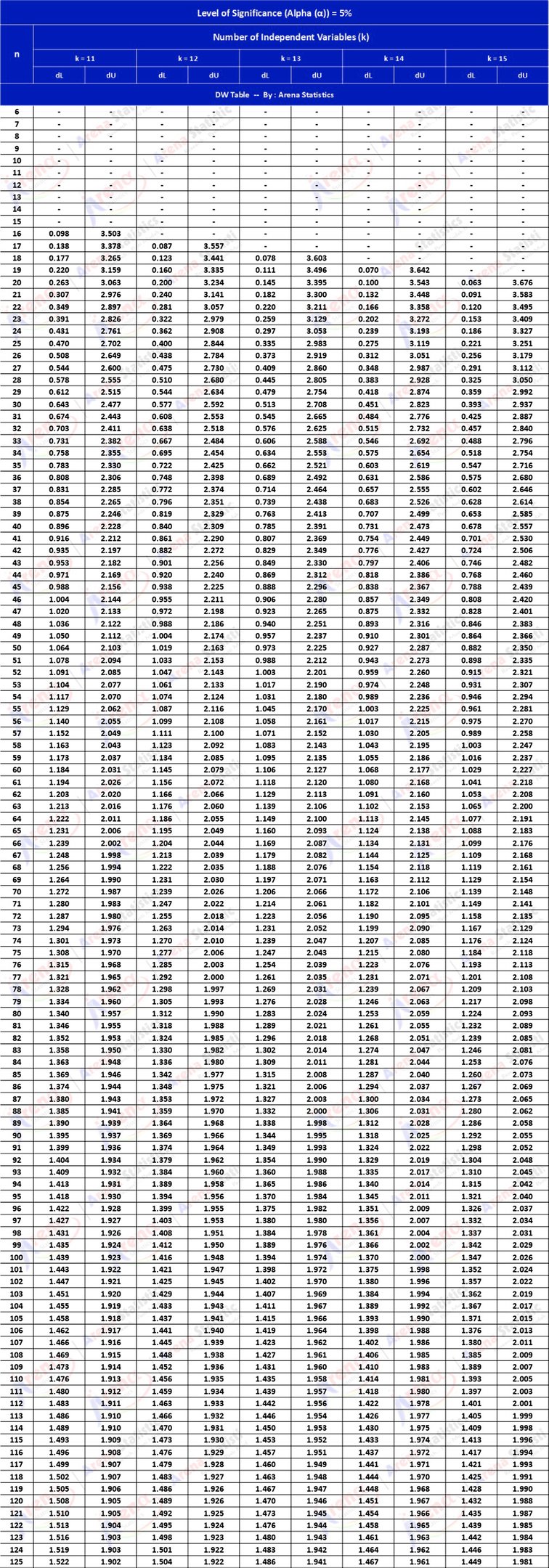
DW Tabel dengan Alpha 5% ; observasi (n) = 6 - 125 ; k = 11 - 15
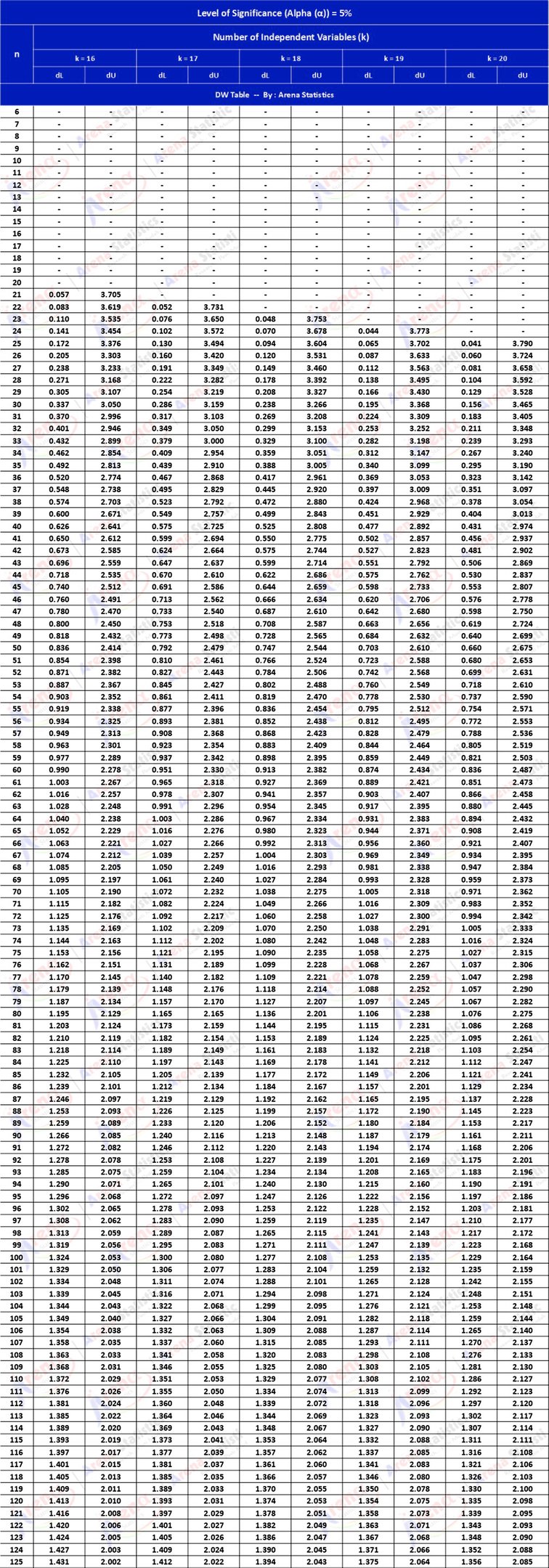
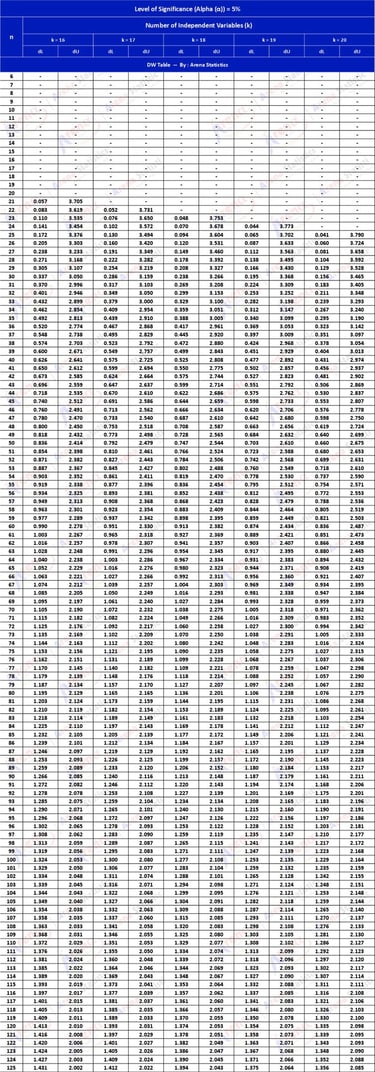
DW Tabel dengan Alpha 5% ; observasi (n) = 6 - 125 ; k = 16 - 20
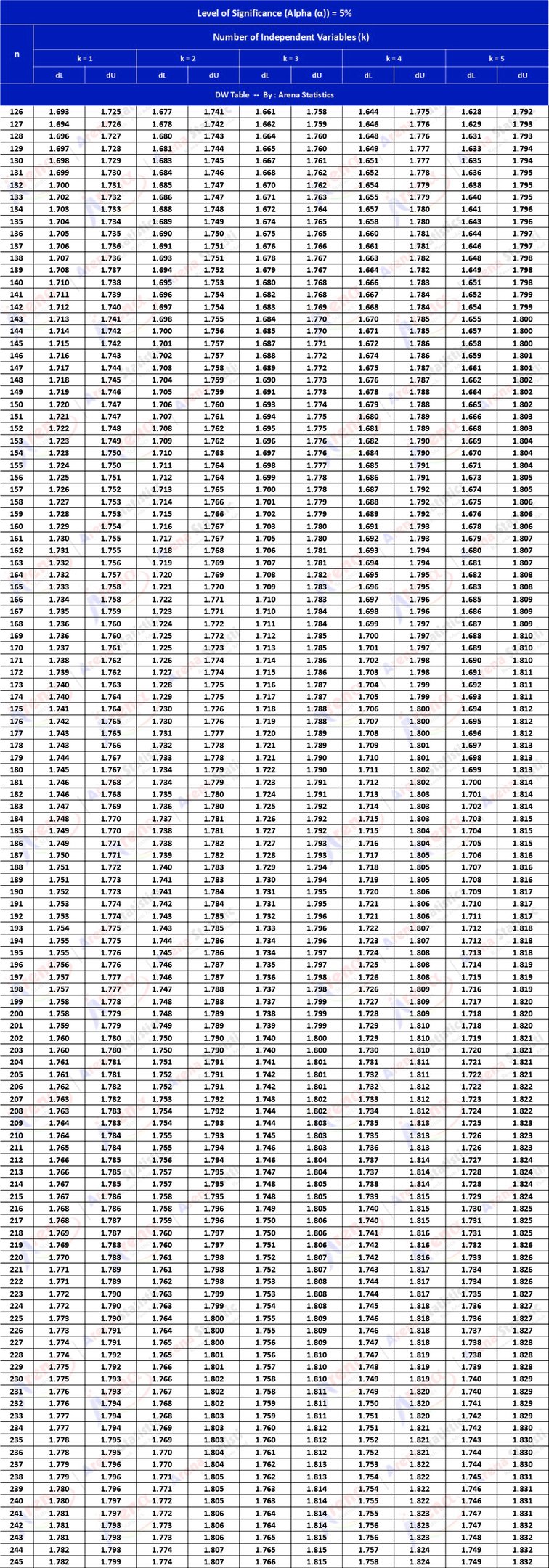
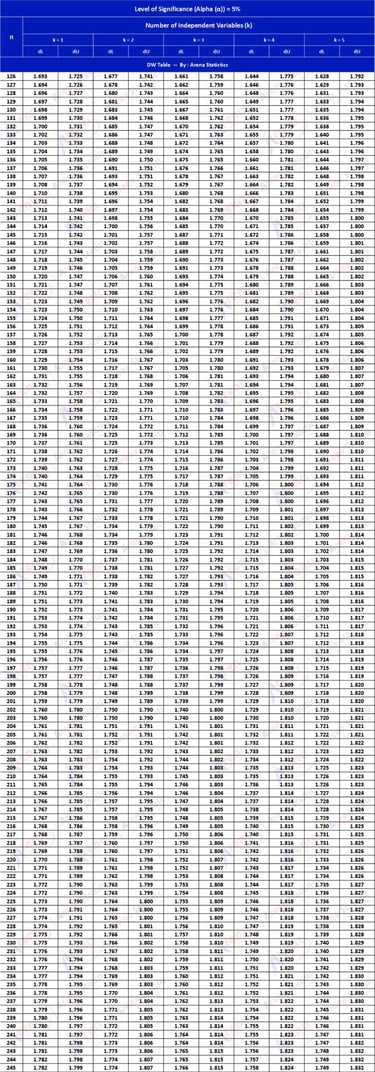
DW Tabel dengan Alpha 5% ; observasi (n) = 126 - 245 ; k = 1 - 5
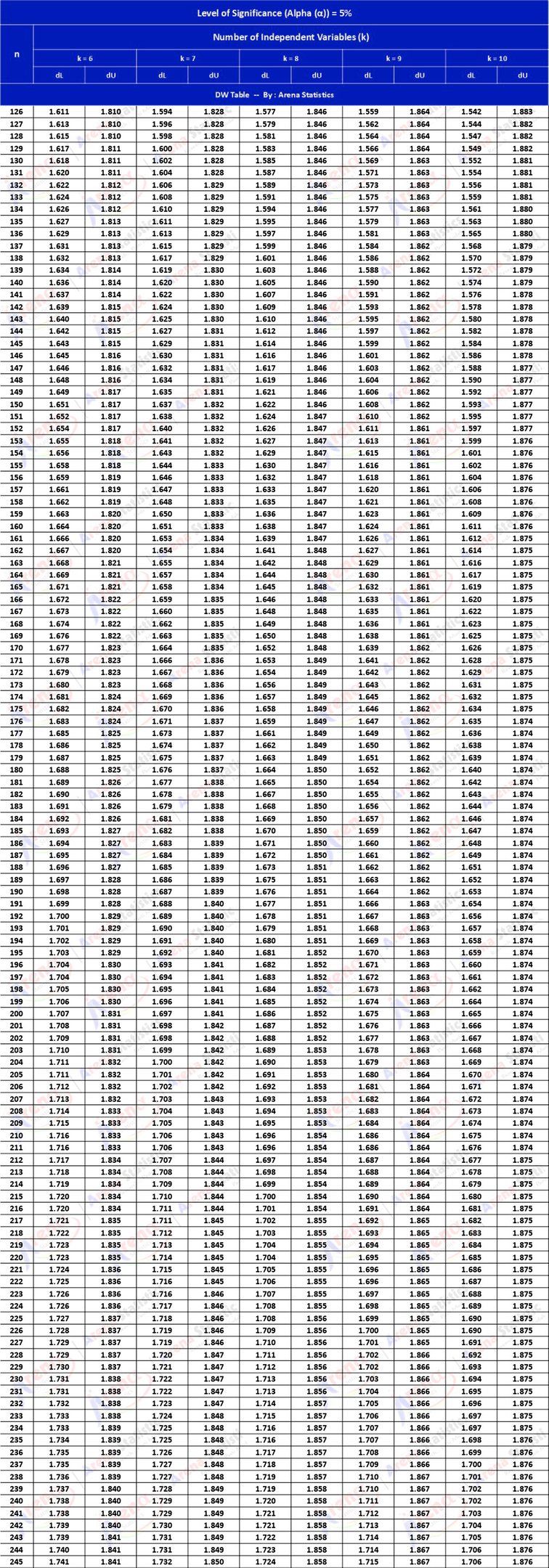
DW Tabel dengan Alpha 5% ; observasi (n) = 126 - 245 ; k = 6 - 10
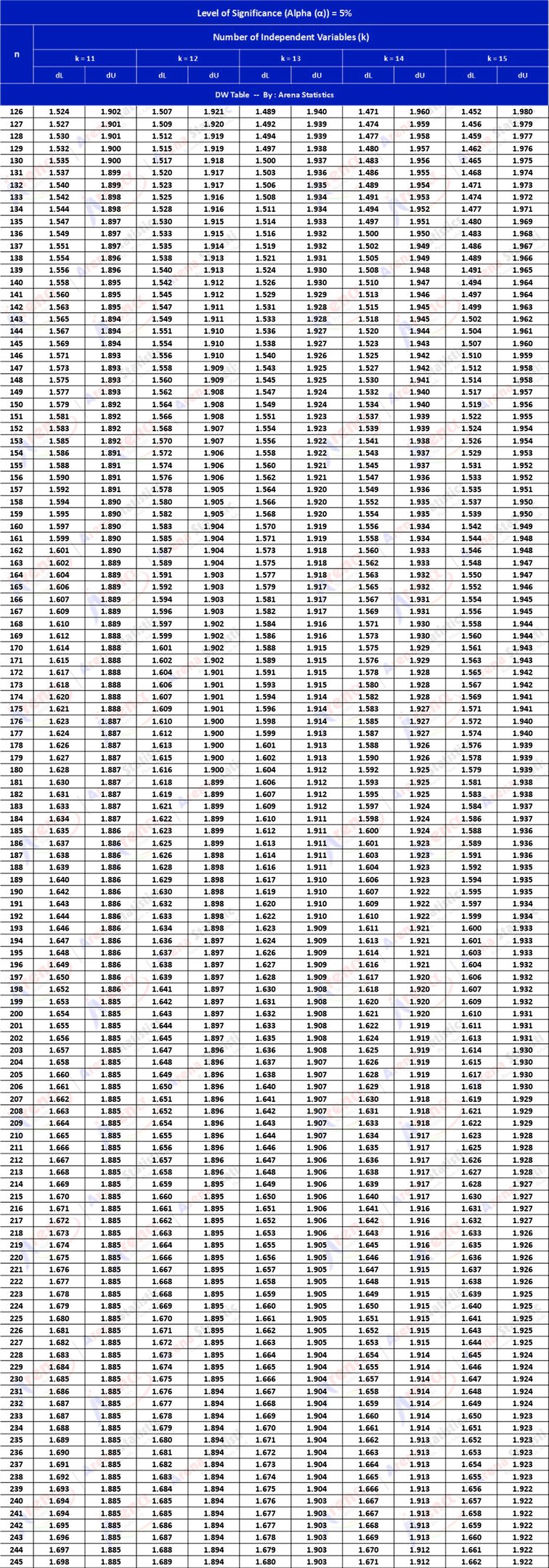
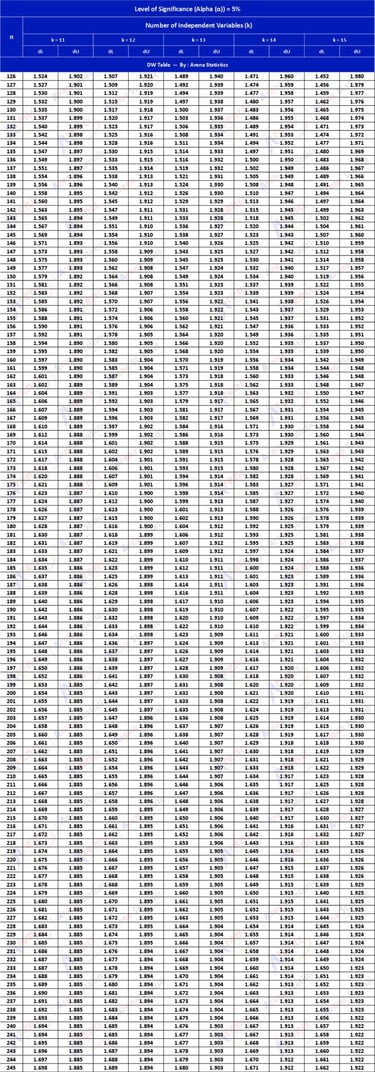
DW Tabel dengan Alpha 5% ; observasi (n) = 126 - 245 ; k = 11 - 15
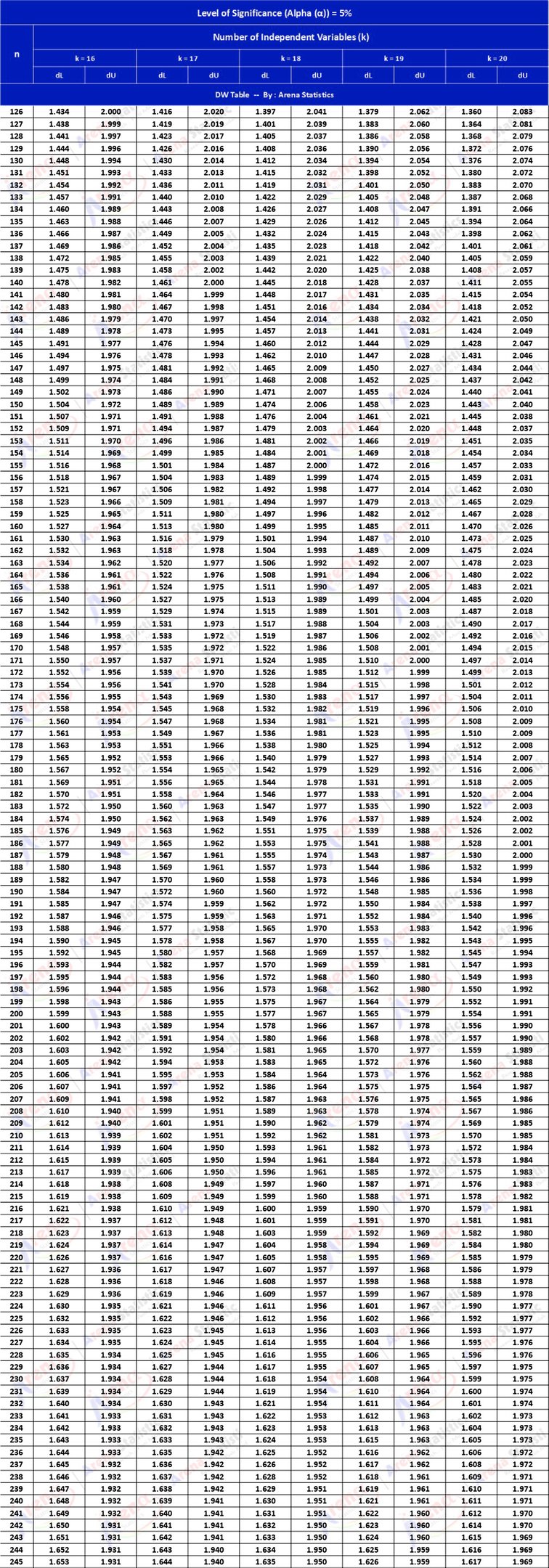
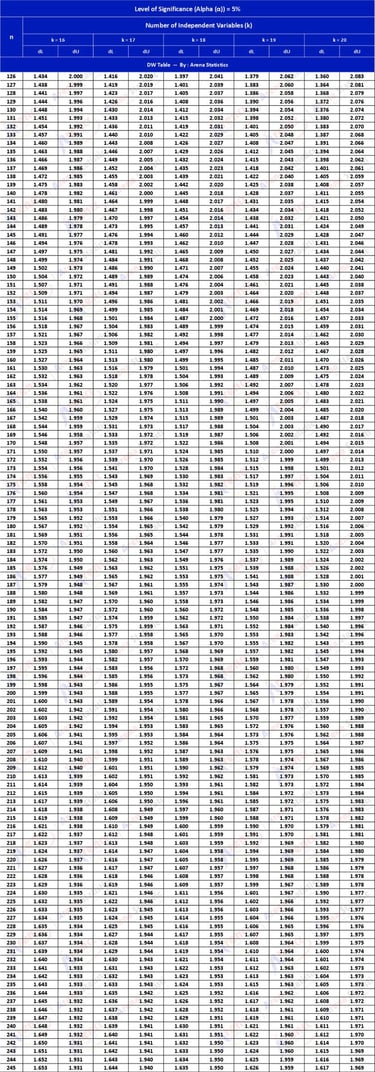
DW Tabel dengan Alpha 5% ; observasi (n) = 126 - 245 ; k = 16 - 20
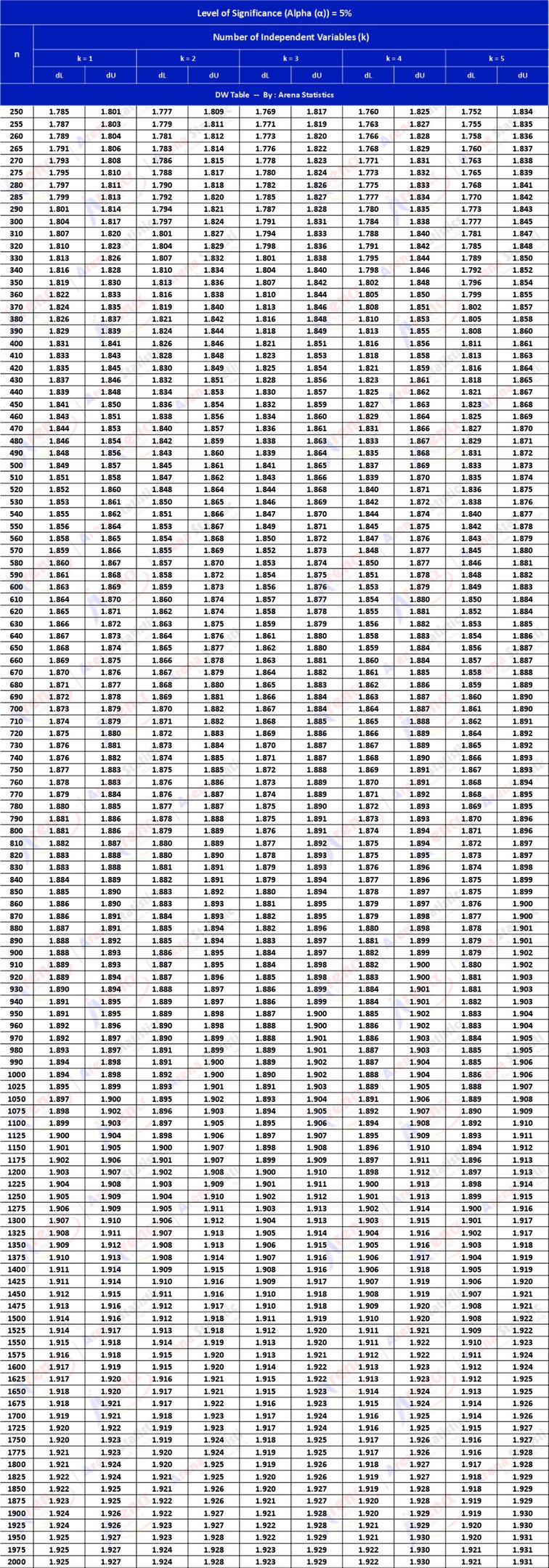
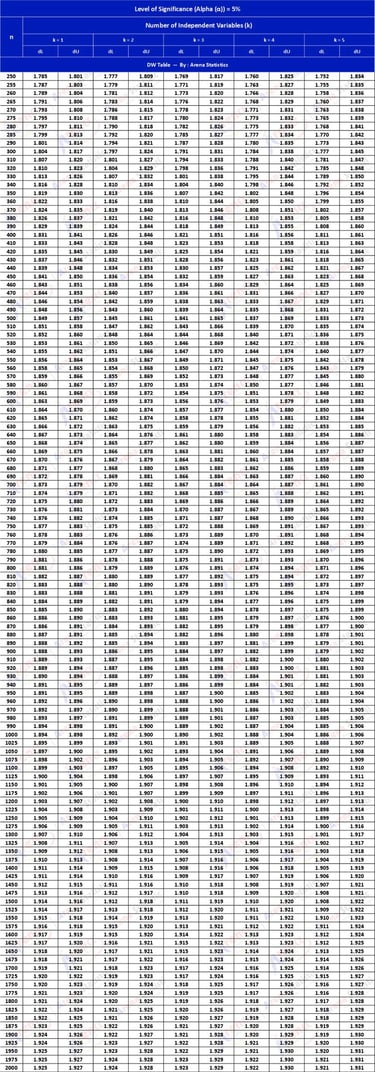
DW Tabel dengan Alpha 5% ; observasi (n) = 250 - 2000 ; k = 1 - 5
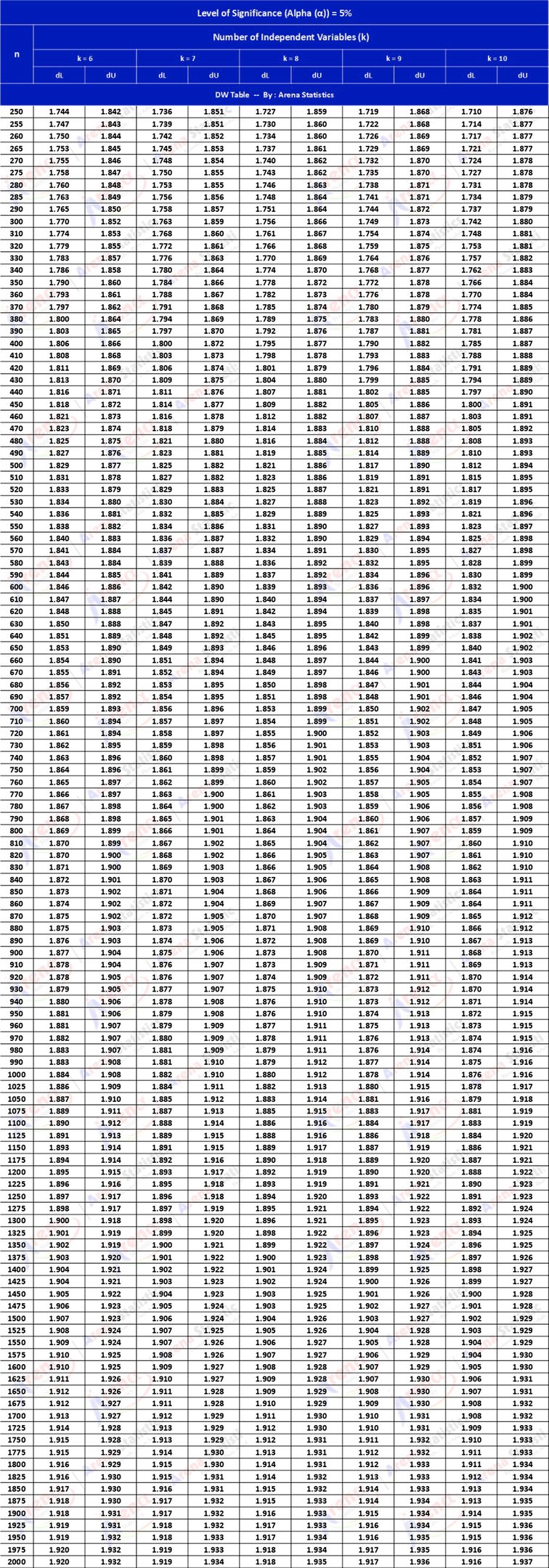
DW Tabel dengan Alpha 5% ; observasi (n) = 250 - 2000 ; k = 6 - 10
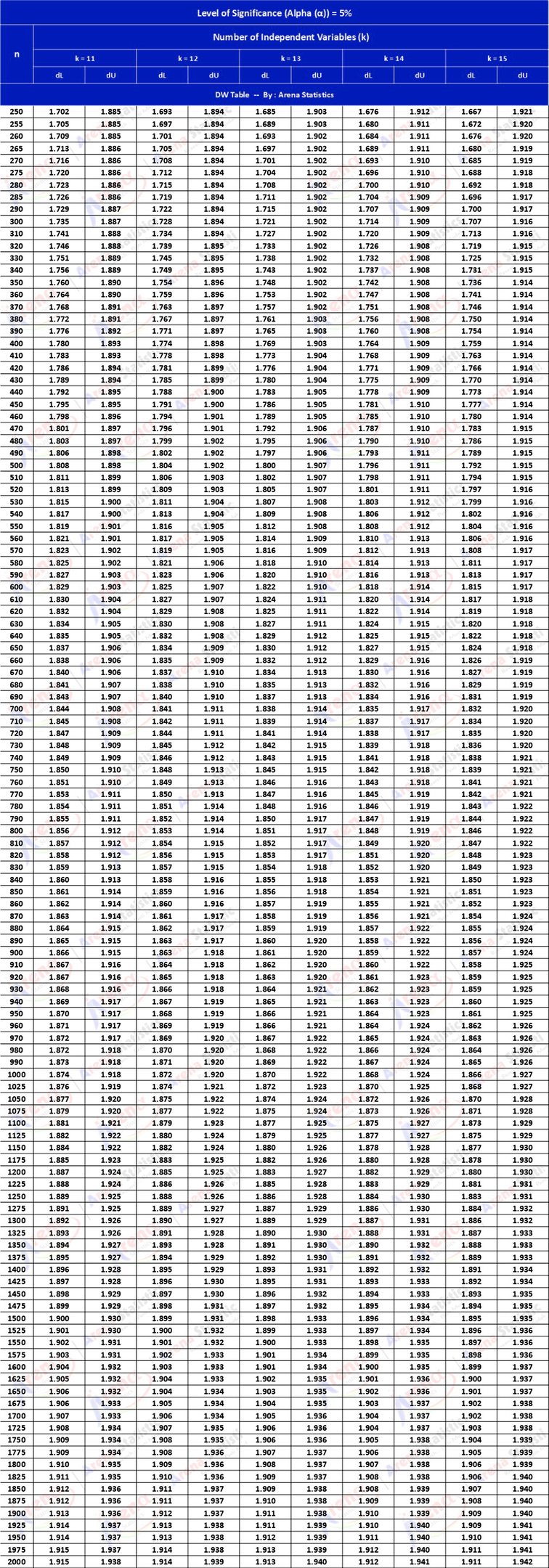
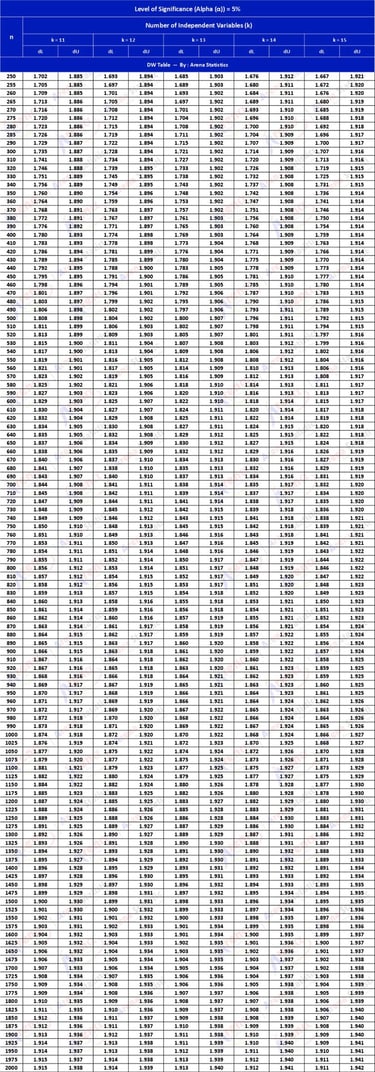
DW Tabel dengan Alpha 5% ; observasi (n) = 250 - 2000 ; k = 11 - 15
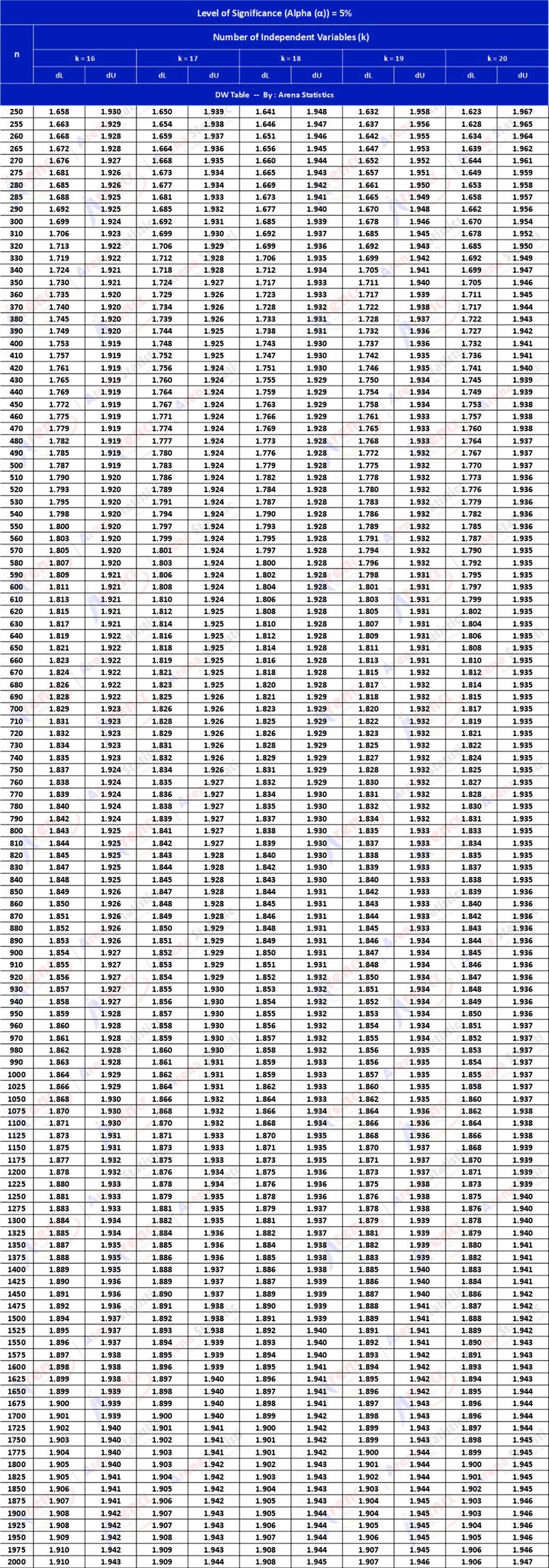
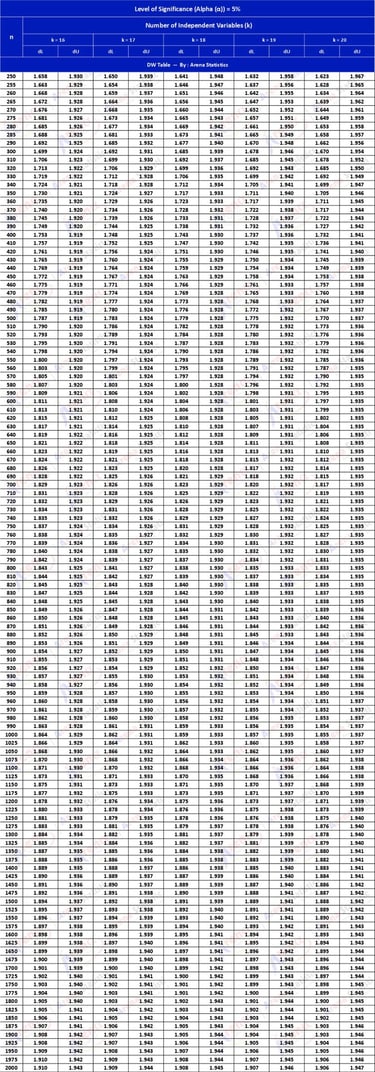
DW Tabel dengan Alpha 5% ; observasi (n) = 250 - 2000 ; k = 16 - 20
Referensi :
Durbin, J. and Watson, G. S. 1950. Testing for Serial Correlation in Least Square Regression. I Biometrika 37 409–428
______________________. 1951. Testing for Serial Correlation in Least Square Regression. II Biometrika 38 159–178
______________________. 1971. Testing for Serial Correlation in Least Square Regression. III Biometrika 58 1–19
Farebrother, R. W. 1980. Algorithm AS 153. Pan's Procedure for The Tail Probabilities of The Durbin–Watson Statistic Applied Statistics 29 224–227
Imhof, J. P. 1961. Computing The Distribution of Quadratic Forms in Normal Variables Biometrika 48 419–426
Newbold, P. 1988. Statistics for Business and Economics Prentice–Hall
Pan, J. J. 1964. Distributions of The Noncircular Serial Correlation Coefficients Shuxue Jinzhan 7 328–337
Gujarati, D.N. and Porter, D.C. 1978. Basic Econometrics. Boston: McGraw-Hill
Gujarati, D.N. 2003. Basic Econometrics. Boston: McGraw-Hill
Lehmann, E. L. 1986. Testing Statistical Hypostheses. New York : John Wiley & Sons.
Walpole, R.E. 1995. Pengantar Statistika, Edisi ke-3, Jakarta : Gramedia Pustaka Utama.
Draper, NR and Smith. 1992.Analisis Regresi Terapan, edisi kedua. Jakarta : Gramedia Pustaka Utama.
Myers, RH.1990. Classical and Modern Regression With Aplications. United States of America : PWS-KENT Publishing Company.
Evans, W. N. 2014. Durbin-Watson significance tables
Kanji, G. K. 2006. 100 Statistical tests. 3rd Ed. SAGE
Neave, H.R. 1978. Statistics Tables for Mathematicians, Engineers, Economists, and The Behavioural and Management Sciences. London : George Allen & Unwin Publisher.
 - versi 2 White-AMqzvNxKRPfRLVOA.png)