 - versi 2 White-AMqzvNxKRPfRLVOA.png)
Calculating Samples Size for Known Population
Populasi Terhingga (Finite) merujuk pada kelompok individu atau objek yang akan diamati dengan jumlah yang dapat ditentukan secara pasti. Artinya, populasi ini memiliki batas jumlah yang jelas dan dapat diketahui secara langsung. Jumlah populasi ini dapat diidentifikasi melalui informan dari institusi atau divisi tertentu, atau dari website tertentu yang terpercaya, seperti BPS, dinas koperasi dan UMKM, Bursa Efek Indonesia, website world population review, dan sebagainya.
Contohnya Populasi Terhingga (Finite Population) :
Masyarakat Kota Malang yang berusia diatas 17 tahun
Mahasiswa Jurusan Statistika di Institute Pertanian Bogor (IPB)
Karyawan yang bekerja di Arena Statistics
Tenaga Kesehatan di Rumah Sakit Arena
Perusahaan perbankan yang listing di BEI periode 2020 - 2024
Kita ambil beberapa contoh untuk kita bahas secara terperinci karakteristik dari subject yang akan kita teliti.
Misal kita ingin meneliti tentang Pengaruh Status Perkawinan terhadap Kesejahteraan Psikologis Perempuan Dewasa di Kota Malang.
Maka populasi yang ingin kita teliti bukan perempuan dewasa di Kota Malang, melainkan sesuai perempuan yang sudah menikah
Masyarakat Kota Malang
Berusia minimal 17 tahun
Berjenis kelamin perempuan
Sudah menikah
maka dari informasi tersebut subject yang kita teliti dapat diketahui jumlah pastinya melalui website BPS maupun malang kota sekitar 366.100 jiwa. Dengan demikian, populasi yang diteliti adalah 336.100 jiwa.
Salah satu teknik perhitungan ukuran sampel minimum dalam penelitian kuantitatif populasi yang diketahui adalah Teknik Estimasi Proporsi pada Populasi Diketahui.
Teknik perhitungan sampel ini hanya digunakan ketika peneliti menggunakan teknik sampling Simple Random Sampling atau Systematic Random Sampling.
by : Nur Asfi Royhan dan Danny Prasetyo Hartanto (2025)
Using The InQuest Calculator
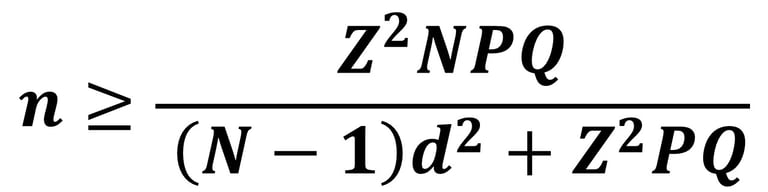
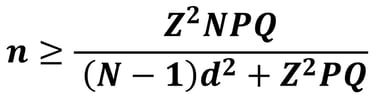
Keterangan :
N = Populasi
Z = Nilai Normal Baku (1.96)
P = proporsi populasi (prevalensi)
Q = 1-P
d = Batas toleransi kesalahan
Catatan Penting!
Proporsi populasi (P) berkaitan erat dengan karakteristik populasi yang diteliti
Proporsi populasi (P) diperoleh dari penelitian terdahulu, atau informasi lain (berita, data BPS, informasi pihak kampus, dll)
Apabila proporsi populasi (p) tidak diketahui, maka peneliti bisa menggunakan default 0.5 (50%)
Penentuan nilai d tidak terlepas dari tingkat representasi ukuran sampel terhadap ukuran populasinya, semakin rendah nilai d maka semakin representatif ukuran sampel terhadap ukuran populasi. Pernyataan ini sejalan dengan Teorema Limit Pusat (Central Limit Theorem) yang berbunyi semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal.
Penulis menyarankan jika populasinya besar atau bahkan terlalu besar (meskipun tidak diketahui jumlahnya) maka peneliti bisa menggunakan nilai d = 1% atau 5%. Sebaliknya jika populasi cenderung kecil maka peneliti bisa menggunakan nilai d = 10%.
Formula Estimasi Proporsi pada Populasi Diketahui dan Besar (N ≥ 10.000)
Formula Estimasi Proporsi pada Populasi Diketahui dan Kecil (N < 10.000)
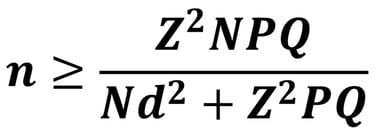
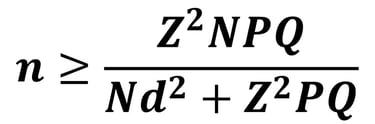
Simulasi 1
Seorang peneliti ingin meneliti UMKM disekitar kampus induk negeri di Kota Malang. (Di Kota Malang ada 3 universitas negeri, yang mana ketiga universitas terletak di kecamatan lowokwaru). Oleh karena itu, karakteristik populasi adalah :
UMKM disekitar kampus induk (Kampus 1) UB, UM, dan UIN
Berlokasi di Kecamatan Lowokwaru, Kota Malang
Kita dapat menemukan informasi banyaknya UMKM yang sesuai dengan karakteristik populasi tersebut di Dinas Koperasi, Perindustrian, dan Perdagangan Kota Malang, sekitar 4.843 UMKM.
Apabila peneliti menggunakan teknik sampling Simple Random Sampling, maka hasil perhitungan banyaknya sampel minimal adalah sebagai berikut :
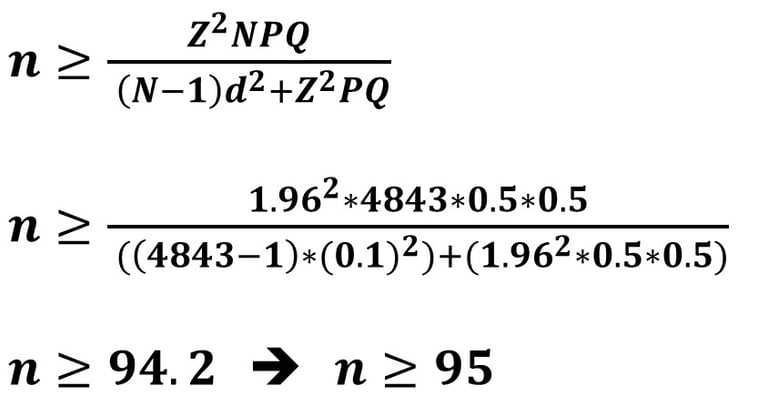
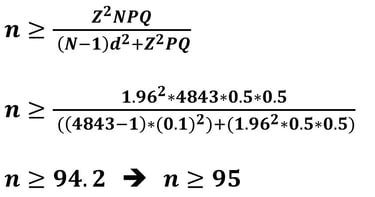
Jika nilai P = 0.5 dan d = 5% (0.05), maka besar sampelnya adalah
Jika nilai P = 0.5 dan d = 10% (0.1), maka besar sampelnya adalah
Simulasi 2
Seorang peneliti ingin mengetahui tingkat kepuasan mahasiswa saintek angkatan 2024 selama satu tahun kuliah di Universitas Indonesia.
Karakteristik populasinya diantaranya :
Mahasiswa Universitas Indonesia
Mahasiswa yang kuliah di Fakultas Saintek
Mahasiswa angkatan tahun 2024
Berdasarkan website BPS, kita dapatkan informasi banyaknya populasi yang sesuai dengan karakteristik tersebut sebanyak 16.259 mahasiswa.
Apabila peneliti menggunakan teknik sampling Simple Random Sampling, maka hasil perhitungan banyaknya sampel minimal adalah sebagai berikut :
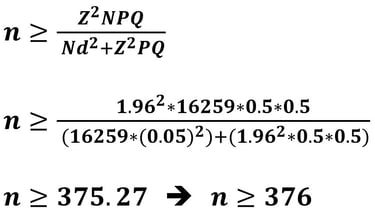
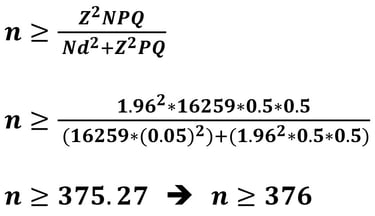
Jika nilai P = 0.5 dan d = 10% (0.1), maka besar sampelnya adalah
Jika nilai P = 0.5 dan d = 5% (0.05), maka besar sampelnya adalah
Untuk mempermudah menghitung sampel dengan formula Estimasi Proporsi pada Populasi Diketahui, peneliti dapat mengakses InQuest Calculator berikut :
Untuk mempermudah menghitung sampel dengan formula Estimasi Proporsi pada Populasi Diketahui, peneliti dapat mengakses InQuest Calculator berikut :
Pembulatan dalam Ukuran Sampel
Apabila kita mencermati hasil ukuran sampel dengan d = 5% diperoleh 375.27 dibulatkan menjadi 376, sementara ukuran sampel dengan d = 10% diperoleh 95.47 dibulatkan menjadi 96. Mengapa semua dibulatkan keatas?
Bukankah secara teori jika desimal ≥ 0.5 seharusnya dibulatkan keatas menjadi 1, dan < 0.5 dibulatkan kebawah menjadi 0?
Teori tersebut memang benar, namun dalam kasus sampel teori ini tidak berlaku. Mengapa?
Alasan 1. Populasi dan sampel terkait dengan sampling unit, bisa individu, bisa organisasi, wilayah, dsb. Kita bayangkan 0.2 individu apakah kita meminta pendapat pada sebagian tubuh manusia, misalkan tangan saja atau kepala saja? tentu tidak masuk akal, maka kita meminta pendapat tubuh yang utuh, sehingga meneliti 0.2 individu sama halnya meneliti 1 individu.
Alasan 2. Kembali pada Teorema Limit Pusat (Central Limit Theorem) bahwa semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal, sehingga apabila peneliti membulatkan kebawah maka sampel menjadi 384 sehingga diperoleh d sebesar 5.03%, sedangkan apabila peneliti membulatkan keatas maka sampel menjadi 385 sehingga diperoleh d sebesar 4.9945%.
d yang diperoleh ketika peneliti membulatkan keatas tentu lebih rendah dibandingkan ketika peneliti membulatkan kebawah, sehingga dengan membulatkan keatas peneliti bisa menggunakan ukuran sampel yang lebih representatif. Dengan demikian,
"Pembulatan dalam ukuran sampel adalah pembulatan keatas"
Referensi :
Cochran, W.G. 1977. Sampling Technique. New York : John Wiley and Sons. Inc
Lemeshow, S., Hosmer Jr., D.W., Klar, J. and Lwanga, S.K. 1990 Adequacy of Sample Size in Health Studies. John Wiley & Sons Ltd., Chichester, 1-5.
Kish, L. 1965. Survey Sampling. New York : John Wiley and Sons, Inc
Machali, I. 2015. Statistik Manajemen Pendidikan, Teori dan Praktik Statistik dalam bidang pendidikan, Penelitian, Ekonomi Bisnis, dan Ilmu-Ilmu Sosial Lainnya. Yogyakarta : Kaukaba Dipantara
Pitard, F.F. 2019. Theory of Sampling and Sampling Practice. Washington D.C. : Chapman and Hall/CRC
Rao, P.S.R.S. 2000. Sampling Methodologies with Applications. Washington D.C. : Chapman and Hall/CRC
Scheaffer, R.L., W. Mendenhall, W. and L. Ott. 1990. Elementary Survey Sampling. 4th Edition. Boston : PWS-KENT Publishing Company
Walpole, R.E. 1995. Pengantar Statistika, Edisi ke-3, Jakarta : Gramedia Pustaka Utama.
Wardhani, N.W.S., Nugroho, W.H., Lusia, dan D.W., Rahmi. 2021. Teknik Sampling dan Survey (Konsep Dasar dan Aplikasi). Malang : UB Press