Stratified Random Sampling

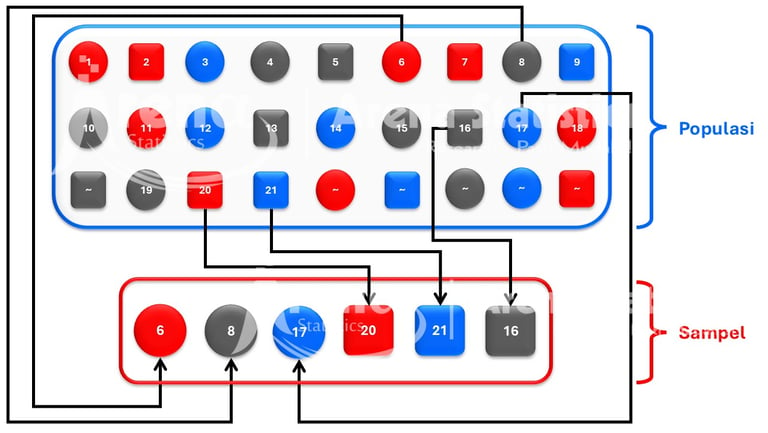
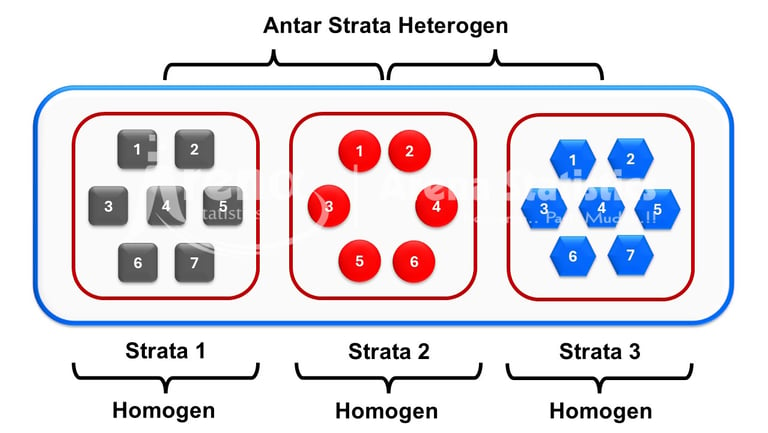
Alokasi Proporsional (Sebanding) merupakan alokasi pada teknik sampling Stratified Random Sampling yang digunakan apabila jumlah populasi antar strata memiliki ukuran yang berbeda  dan ragam tiap strata tidak jauh berbeda. Dengan menggunakan alokasi proporsional maka peneliti bisa mendapatkan sampel secara proporsional berdasarkan banyak populasi disetiap strata, misal, strata A populasinya lebih tinggi dibanding strata B, maka sampel yang akan diambil di strata A juga lebih tinggi dibandingkan sampel di strata B.

Formula ukuran sampel minimum pada stratified random sampling dengan alokasi proporsional (sebanding) : 

Keterangan :

n   = Sampel minimum keseluruhan strata

N   = Populasi keseluruhan

Nh = Populasi pada strata h

Ph = Proporsi populasi pada strata h

Qh = 1 - Ph

d   = Batas toleransi kesalahan

Z   = Nilai Normal Baku (1.96)

Catatan Penting!

• Proporsi populasi per strata (Ph) berkaitan erat dengan karakteristik populasi yang diteliti

• Proporsi populasi per strata (Ph) diperoleh dari penelitian terdahulu, atau informasi lain (berita, data BPS, informasi pihak kampus, dll)

• Apabila proporsi populasi per strata (ph) tidak diketahui, maka peneliti bisa menggunakan default 0.5 (50%)

• Penentuan nilai d tidak terlepas dari tingkat representasi ukuran sampel terhadap ukuran populasinya, semakin rendah nilai d maka semakin representatif ukuran sampel terhadap ukuran populasi. Pernyataan ini sejalan dengan Teorema Limit Pusat (Central Limit Theorem) yang berbunyi semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal.

  Penulis menyarankan jika populasinya besar atau bahkan terlalu besar (meskipun tidak diketahui jumlahnya) maka peneliti bisa menggunakan nilai d = 1% atau 5%. Sebaliknya jika populasi cenderung kecil maka peneliti bisa menggunakan nilai d = 10%.

Setelah diperoleh ukuran sampel minimum, kemudian kita hitung sampel per strata menggunakan Formula berikut :

Keterangan :

nh = Sampel pada Strata h

Nh = Populasi pada Strata h

N = Populasi keseluruhan

n = Sampel minimum keseluruhan strata

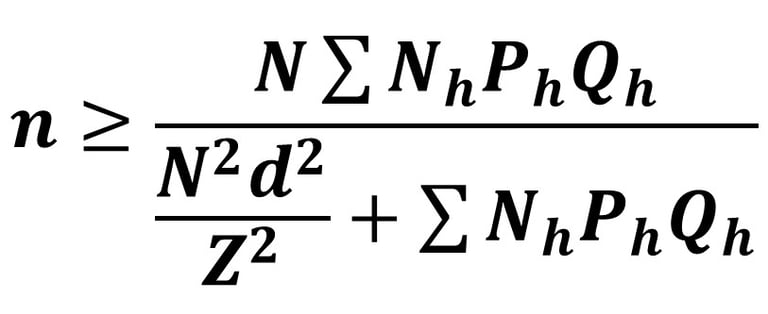
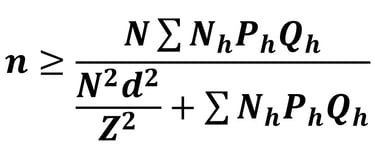
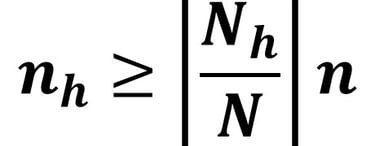
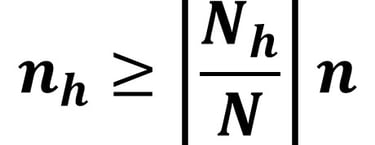
Contoh :

Penelitian tentang gaya hidup karyawan PT Arena Inc. Karyawan PT Arena Inc sebanyak 2500 orang, dimana diklasifikasikan berdasarkan 4 strata masa kerja.

Strata 1 : Karyawan lama dengan masa kerja lebih dari 10 tahun (300)

Strata 2 : Karyawan lama dengan masa kerja 5 - 10 tahun (700 orang)

Strata 3 : Karyawan baru dengan masa kerja 1 - 5 tahun (900 orang)

Strata 4 : Karyawan training dengan masa kerja kurang dari 1 tahun (600 orang)

Note :

Perhitungan sampel minimum keseluruhan strata jika menggunakan alokasi proporsional dengan batas toleransi kesalahan 5%

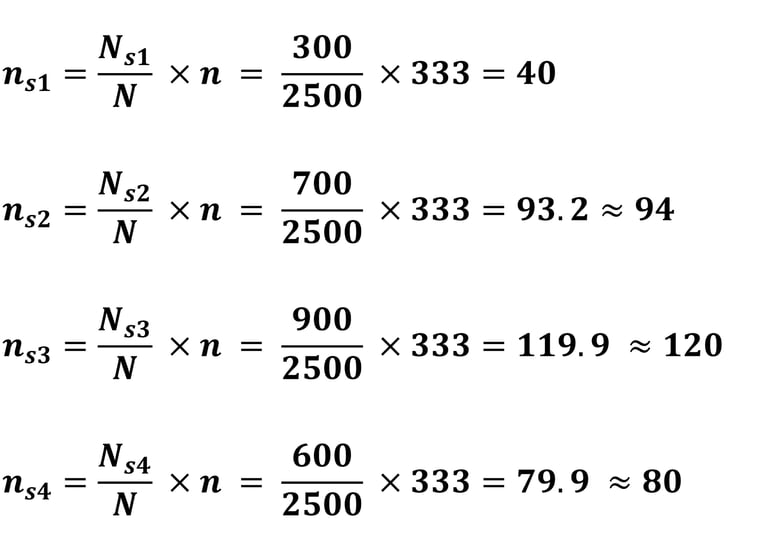
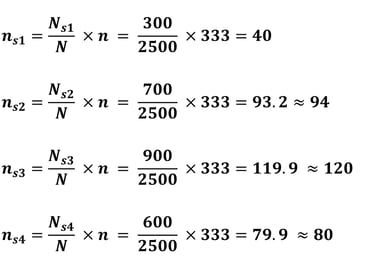
Setelah kita peroleh ukuran sampel minimum keseluruhan, selanjutnya kita hitung sampel pada masing-masing strata.

Apabila dijumlahkan sampelnya menjadi 334 (Hal ini wajar karena dalam perhitungan sampel, aturan pembulatan harus pembulatan keatas, sehingga sampel hasil perhitungan alokasi proporsional menjadi lebih besar dibandingkan sampel yang sudah dihitung (333). Karena semakin besar sampel yang digunakan maka semakin representatif (Central Limit Theorem). Jadi sampel minimum keseluruhan yang harus dipenuhi oleh peneliti bukan lagi 333, melainkan 334.

Untuk mempermudah menghitung sampel menggunakan alokasi proporsional, peneliti dapat mengakses InQuest Calculator berikut :

Pembulatan dalam Ukuran Sampel

Apabila kita mencermati hasil ukuran sampel dengan d = 5% diperoleh 93.2 dibulatkan menjadi 94. Mengapa sampel tersebut dibulatkan keatas?

Bukankah secara teori jika desimal ≥ 0.5 seharusnya dibulatkan keatas menjadi 1, dan < 0.5 dibulatkan kebawah menjadi 0?

Teori tersebut memang benar, namun dalam kasus sampel teori ini tidak berlaku. Mengapa?

Alasan 1. Populasi dan sampel terkait dengan sampling unit, bisa individu, bisa organisasi, wilayah, dsb. Kita bayangkan 0.2 individu apakah kita meminta pendapat pada sebagian tubuh manusia, misalkan tangan saja atau kepala saja? tentu tidak masuk akal, maka kita meminta pendapat tubuh yang utuh, sehingga meneliti 0.2 individu sama halnya meneliti 1 individu.

Alasan 2. Kembali pada Teorema Limit Pusat (Central Limit Theorem) bahwa semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal, sehingga apabila peneliti membulatkan kebawah maka sampel menjadi 384 sehingga diperoleh d sebesar 5.03%, sedangkan apabila peneliti membulatkan keatas maka sampel menjadi 385 sehingga diperoleh d sebesar 4.9945%.

d yang diperoleh ketika peneliti membulatkan keatas tentu lebih rendah dibandingkan ketika peneliti membulatkan kebawah, sehingga dengan membulatkan keatas peneliti bisa menggunakan ukuran sampel yang lebih representatif. Dengan demikian,

"Pembulatan dalam ukuran sampel adalah pembulatan keatas"

Referensi :

• Cochran, W.G. 1977. Sampling Technique. New York : John Wiley and Sons. Inc

• Kish, L. 1965. Survey Sampling. New York : John Wiley and Sons, Inc

• Machali, I. 2015. Statistik Manajemen Pendidikan, Teori dan Praktik Statistik dalam bidang pendidikan, Penelitian, Ekonomi Bisnis, dan Ilmu-Ilmu Sosial Lainnya. Yogyakarta : Kaukaba Dipantara

• Pitard, F.F. 2019. Theory of Sampling and Sampling Practice. Washington D.C. : Chapman and Hall/CRC

• Rao, P.S.R.S. 2000. Sampling Methodologies with Applications. Washington D.C. : Chapman and Hall/CRC

• Scheaffer, R.L., W. Mendenhall, W. and L. Ott. 1990. Elementary Survey Sampling. 4th Edition. Boston : PWS-KENT Publishing Company

• Solimun, Fernandes, A.A.R., Nurjannah. 2017. Metode Statistika Multivariat Pemodelan Persamaan Struktural (SEM) Pendekatan WarpPLS. Malang : UB Press

• Walpole, R.E. 1995. Pengantar Statistika, Edisi ke-3, Jakarta : Gramedia Pustaka Utama.

• Wardhani, N.W.S., Nugroho, W.H., Lusia, dan D.W., Rahmi. 2021. Teknik Sampling dan Survey (Konsep Dasar dan Aplikasi). Malang : UB Press