Calculating Samples Size for UnKnown Population
Populasi Tak Terhingga (Infinite) adalah populasi yang jumlah tidak dapat diidentifikasi secara pasti, jelas dan mudah. Dengan kata lain jumlah populasi tersebut tidak terbatas (Infinite) atau tidak diketahui (UnKnown), bisa populasi memiliki jumlah yang terlalu besar atau kecil namun tidak dapat teridentifikasi secara jelas.
Contohnya :
Masyarakat yang pernah berbelanja online melalui website belanja online (marketplace)
Mahasiswa Universitas Indonesia yang menggunakan iPhone
Masyarakat yang terdiagnosis mengalami penyakit gerd.
Ibu hamil yang mengikuti senam hamil
Mahasiswa perempuan Fakultas Ekonomi dan Bisnis Universitas Brawijaya yang menjadi entrepreneur dan menggunakan QRIS sebagai sistem pembayaran
Kita ambil salah satu contoh (contoh terakhir) untuk kita bahas secara terperinci karakteristik dari subject yang akan kita teliti.
Karakteristik populasinya diantaranya :
Mahasiswa berjenis kelamin perempuan
Kuliah di Fakultas Ekonomi dan Bisnis Universitas Brawijaya
Menjadi entrepreneur
Menggunakan QRIS sebagai sistem pembayaran
maka dari informasi tersebut subject yang kita teliti tidak dapat diketahui jumlah pastinya. Kalau pun dicari pada bagian akademik juga tidak akan tersedia informasi sesuai dengan karakteristik populasi. Sehingga populasi seperti contoh di atas adalah termasuk fenomena yang mana populasi yang diamati tidak dapat diketahui secara pasti jumlahnya.
Oleh karena itu, akan ada dua pertanyaan yang sering muncul adalah
Bagaimana cara menentukan jumlah sampelnya?
Apakah sampel yang didapat bisa representatif?
Besarnya ukuran sampel yang diperoleh pada populasi tak terhingga tidak akan pernah representatif. Hal ini dikarenakan jumlah populasi yang tidak diketahui tidak dapat diukur tingkat representatifnya, namun peneliti tetap bisa mengupayakan agar representative berdasarkan pertimbangan rasional peneliti. Salah satu teknik perhitungan ukuran sampel minimum dalam penelitian kuantitatif populasi yang tidak diketahui secara pasti jumlahnya adalah Teknik Estimasi Proporsi pada Populasi Tidak Diketahui.
by : Danny Prasetyo Hartanto (2025)
Using The InQuest Calculator
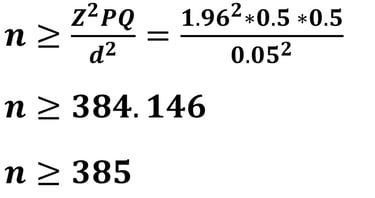
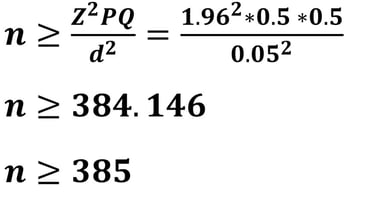
Apabila kita memperhatikan ukuran sampel minimum dengan nilai d sebesar 5% jauh lebih tinggi daripada menggunakan nilai d sebesar 10%. Coba kita evaluasi.! apakah dengan sampel minimum 375 (simulasi 1) dan 167 (simulasi 2) peneliti bisa mendapatkannya semua? Mungkin akan sulit didapatkan, maka untuk mempermudah penelitian (sesuai prinsip parsimony) maka sebaiknya peneliti menggunakan nilai d sebesar 10% sehingga diperoleh ukuran sampel yang tidak terlalu tinggi.
Untuk mempermudah menghitung formula Estimasi Proporsi pada Populasi Tidak Diketahui, peneliti dapat mengakses InQuest Calculator berikut :
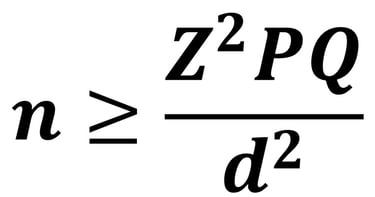
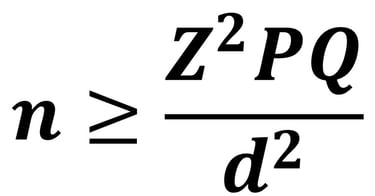
Keterangan :
Z = Nilai Normal Baku (1.96)
P = proporsi populasi (prevalensi)
Q = 1-P
d = Batas toleransi kesalahan
Catatan Penting!
Proporsi populasi (P) berkaitan erat dengan karakteristik populasi yang diteliti
Proporsi populasi (P) diperoleh dari penelitian terdahulu, atau informasi lain (berita, data BPS, informasi pihak kampus, dll)
Apabila proporsi populasi (p) tidak diketahui, maka peneliti bisa menggunakan default 0.5 (50%)
Penentuan nilai d tidak terlepas dari tingkat representasi ukuran sampel terhadap ukuran populasinya, semakin rendah nilai d maka semakin representatif ukuran sampel terhadap ukuran populasi. Pernyataan ini sejalan dengan Teorema Limit Pusat (Central Limit Theorem) yang berbunyi semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal.
Penulis menyarankan jika populasinya besar atau bahkan terlalu besar (meskipun tidak diketahui jumlahnya) maka peneliti bisa menggunakan nilai d = 1% atau 5%. Sebaliknya jika populasi cenderung kecil maka peneliti bisa menggunakan nilai d = 10%.
Simulasi 1
Kita gunakan contoh nomor 5 yang kita telah bahas sebelumnya.
1. Mahasiswa berjenis kelamin perempuan
2. Kuliah di Fakultas Ekonomi dan Bisnis Universitas Brawijaya
3. Menjadi entrepreneur
4. Menggunakan QRIS sebagai sistem pembayaran
Karena kita tidak menemukan informasi apapun, maka nilai proporsi populasi (P) yang kita gunakan adalah 0.5 (50%).
Jika nilai d = 5% (0.05), maka besar sampelnya adalah
Jika nilai d = 10% (0.1), maka besar sampelnya adalah
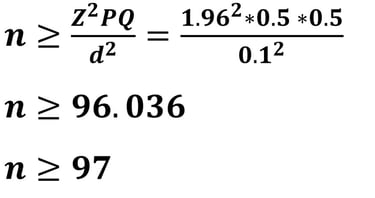
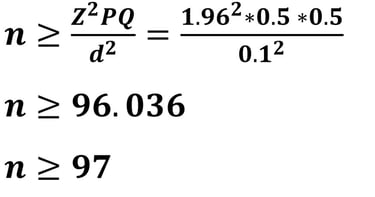
Simulasi 2
Kita gunakan contoh nomor 2 (Mahasiswa Universitas Indonesia yang menggunakan iPhone)
Karakteristik populasinya diantaranya :
1. Mahasiswa Universitas Indonesia (semua jurusan)
2. Menggunakan Iphone
Karena kita tidak menemukan informasi mengenai jumlah populasi, namun kita menemukan informasi proporsi populasi melalui berita dari website (https://katadata.co.id/infografik/673d532984f6c/infografik-pasar-apple-di-indonesia-makin-sulit) berikut :


Dari berita tersebut, kita mendapatkan informasi pangsa pasar iPhone di Indonesia sebesar 12.4%. Apabila kita asumsikan pangsa pasar iPhone di Universitas Indonesia tidak jauh berbeda dengan pangsa pasar iPhone di Indonesia, maka kita bisa menggunakan nilai proporsi populasi (prevalensi) berdasarkan informasi dalam berita tersebut, yaitu 12.4% (0.124).
Jika nilai d = 10% (0.1), maka besar sampelnya adalah
Jika nilai d = 5% (0.05), maka besar sampelnya adalah
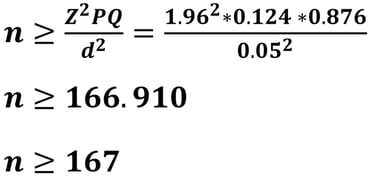
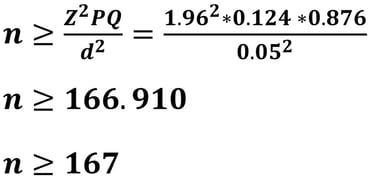
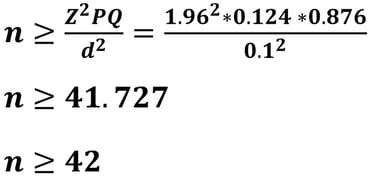
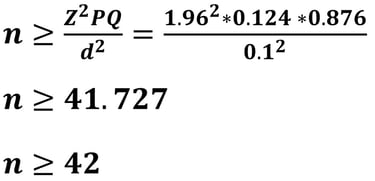
Pembulatan dalam Ukuran Sampel
Apabila kita mencermati hasil ukuran sampel dengan d = 5% diperoleh 384.146 dibulatkan menjadi 385, sementara ukuran sampel dengan d = 10% diperoleh 96.036 dibulatkan menjadi 97. Mengapa semua dibulatkan keatas?
Bukankah secara teori jika desimal ≥ 0.5 seharusnya dibulatkan keatas menjadi 1, dan < 0.5 dibulatkan kebawah menjadi 0?
Teori tersebut memang benar, namun dalam kasus sampel teori ini tidak berlaku. Mengapa?
Alasan 1. Populasi dan sampel terkait dengan sampling unit, bisa individu, bisa organisasi, wilayah, dsb. Kita bayangkan 0.2 individu apakah kita meminta pendapat pada sebagian tubuh manusia, misalkan tangan saja atau kepala saja? tentu tidak masuk akal, maka kita meminta pendapat tubuh yang utuh, sehingga meneliti 0.2 individu sama halnya meneliti 1 individu.
Alasan 2. Kembali pada Teorema Limit Pusat (Central Limit Theorem) bahwa semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal, sehingga apabila peneliti membulatkan kebawah maka sampel menjadi 384 sehingga diperoleh d sebesar 5.03%, sedangkan apabila peneliti membulatkan keatas maka sampel menjadi 385 sehingga diperoleh d sebesar 4.9945%.
d yang diperoleh ketika peneliti membulatkan keatas tentu lebih rendah dibandingkan ketika peneliti membulatkan kebawah, sehingga dengan membulatkan keatas peneliti bisa menggunakan ukuran sampel yang lebih representatif. Dengan demikian,
"Pembulatan dalam ukuran sampel adalah pembulatan keatas"
Referensi :
Cochran, W.G. 1977. Sampling Technique. New York : John Wiley and Sons. Inc
Lemeshow, S., Hosmer Jr., D.W., Klar, J. and Lwanga, S.K. 1990 Adequacy of Sample Size in Health Studies. John Wiley & Sons Ltd., Chichester, 1-5.
Kish, L. 1965. Survey Sampling. New York : John Wiley and Sons, Inc
Machali, I. 2015. Statistik Manajemen Pendidikan, Teori dan Praktik Statistik dalam bidang pendidikan, Penelitian, Ekonomi Bisnis, dan Ilmu-Ilmu Sosial Lainnya. Yogyakarta : Kaukaba Dipantara
Pitard, F.F. 2019. Theory of Sampling and Sampling Practice. Washington D.C. : Chapman and Hall/CRC
Rao, P.S.R.S. 2000. Sampling Methodologies with Applications. Washington D.C. : Chapman and Hall/CRC
Scheaffer, R.L., W. Mendenhall, W. and L. Ott. 1990. Elementary Survey Sampling. 4th Edition. Boston : PWS-KENT Publishing Company
Walpole, R.E. 1995. Pengantar Statistika, Edisi ke-3, Jakarta : Gramedia Pustaka Utama.
Wardhani, N.W.S., Nugroho, W.H., Lusia, dan D.W., Rahmi. 2021. Teknik Sampling dan Survey (Konsep Dasar dan Aplikasi). Malang : UB Press
 - versi 2 White-AMqzvNxKRPfRLVOA.png)